题目内容
4.已知函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{3}x|}&{0<x<3}\\{sin\frac{πx}{6}}&{3≤x≤15}\end{array}\right.$,若直线y=m(m∈R)与函数f(x)的图象有四个交点,且交点的横坐标从小到大依次为a,b,c,d,则$\frac{(c-1)(d-1)}{ab}$的取值范围是(28,55).分析 作出函数f(x)的图象,根据图象可得:①ab=1;②c+d=18;③c∈(3,6),d∈(12,15),再求出$\frac{(c-1)(d-1)}{ab}$的取值范围.
解答 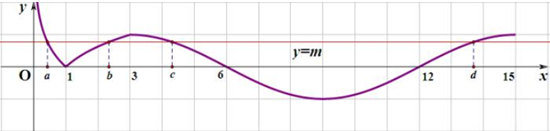 解:根据图象可得:
解:根据图象可得:
①ab=1;
②c+d=18;
③c∈(3,6),d∈(12,15),
因此则$\frac{(c-1)(d-1)}{ab}$=(c-1)•(d-1)=cd-(c+d)+1=-(c-9)2+64∈(28,55).
故答案为:(28,55).
点评 本题考查分段函数,考查数形结合的数学思想,正确作出函数的图象是关键.

练习册系列答案
相关题目
9.已知函数y=eax+3x有平行于x轴的切线且切点在y轴右侧,则a的范围为( )
| A. | (-∞,-3) | B. | (-∞,3) | C. | (3,+∞) | D. | (-3,+∞) |
 一个单摆如图所示,角(弧度)从竖直开始移动作为时间(秒)的函数满足f(x)=$\frac{1}{2}$sin(2t+$\frac{π}{2}$).求:多长时间单摆完成5次完整摆动?
一个单摆如图所示,角(弧度)从竖直开始移动作为时间(秒)的函数满足f(x)=$\frac{1}{2}$sin(2t+$\frac{π}{2}$).求:多长时间单摆完成5次完整摆动?