题目内容
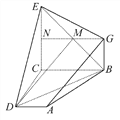
【题目】如图，已知四边形ABCD和BCEG均为直角梯形，AD∥BC，CE∥BG，且∠BCD=∠BCE=90°，平面ABCD⊥平面BCEG，BC=CD=CE=2AD=2BG.
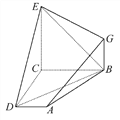
(1)求证：EC⊥CD.
(2)求证：AG∥平面BDE.
【答案】详见解析
【解析】试题分析：（Ⅰ）利用面面垂直的性质，证明EC⊥平面ABCD，利用线面垂直的性质证明EC⊥CD；
（Ⅱ）在平面BCEG中，过G作GN⊥CE交BE于M，连DM，证明四边形ADMG为平行四边形，可得AG∥DM，即可证明AG∥平面BDE.
试题解析：
(1)由平面ABCD⊥平面BCEG，
平面ABCD∩平面BCEG=BC，CE⊥BC，CE平面BCEG，
所以EC⊥平面ABCD，又CD平面ABCD，故EC⊥CD.
(2)在平面BCEG中，过G作GN⊥CE交BE于M，连接DM，则由已知知，MG=MN，MN∥BC∥DA，且MN=AD=
BC，
所以MG∥AD，MG=AD，
故四边形ADMG为平行四边形，
所以AG∥DM，因为DM平面BDE，AG平面BDE，所以AG∥平面BDE.
练习册系列答案
相关题目
