题目内容
15.在直径AB为2的圆上有长度为1的动弦CD,则$\overrightarrow{AC}$•$\overrightarrow{BD}$的取值范围是[-$\frac{3}{2}$,$\frac{1}{2}$].分析 建立直角坐标系,设出∠BOC=x,用x表示C,D的坐标,求出$\overrightarrow{AC}$•$\overrightarrow{BD}$,然后化简,即可求解它的范围.
解答 解:如图建立平面直角坐标系: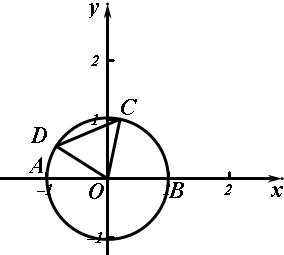 设∠BOC=x,则C(cosx,sinx),∠BOD=x+60°,D(cos(x+60°),sin(x+60°)),A(-1,0),B(1,0),
设∠BOC=x,则C(cosx,sinx),∠BOD=x+60°,D(cos(x+60°),sin(x+60°)),A(-1,0),B(1,0),
则$\overrightarrow{AC}$=(cosx+1,sinx),$\overrightarrow{BD}$=(cos(x+60°)-1,sin(x+60°)),
则$\overrightarrow{AC}$•$\overrightarrow{BD}$=(cosx+1)[cos(x+60°)-1]+sinxsin(x+60°)
=cosxcos(x+60°)-cosx+cos(x+60°)-1+sinxsin(x+60°)
=cos60°-cosx+cos(x+60°)-1
=-cos(x-60°)-$\frac{1}{2}$,
所以$\overrightarrow{AC}$•$\overrightarrow{BD}$的取值范围是[-$\frac{3}{2}$,$\frac{1}{2}$];
故答案为:[-$\frac{3}{2}$,$\frac{1}{2}$].
点评 本题考查向量数量积的应用,考查转化思想计算能力,建立直角坐标系,利用坐标运算是解答本题的关键.

练习册系列答案
相关题目
6.曲线y=x2+2x在点(1,3)处的切线方程是( )
| A. | 4x-y-1=0 | B. | 3x-4y+1=0 | C. | 3x-4y+1=0 | D. | 4y-3x+1=0 |