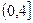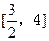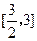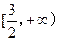题目内容
已知二次函数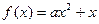 (
(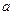
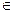 R,
R,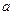
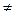 0).(1)当0<
0).(1)当0<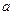 <
<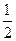 时,
时,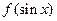 (
(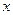
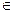 R)的最大值为
R)的最大值为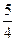 ,求
,求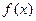 的最小值.(2)如果
的最小值.(2)如果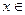 [0,1]时,总有|
[0,1]时,总有|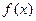 |
|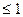 .试求
.试求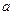 的取值范围.(3)令
的取值范围.(3)令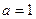 ,当
,当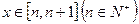 时,
时,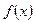 的所有整数值的个数为
的所有整数值的个数为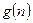 ,求证数列
,求证数列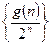 的前
的前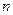 项的和
项的和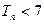 .
.
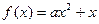 (
(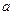
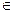 R,
R,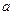
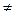 0).(1)当0<
0).(1)当0<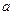 <
<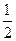 时,
时,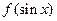 (
(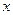
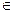 R)的最大值为
R)的最大值为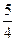 ,求
,求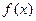 的最小值.(2)如果
的最小值.(2)如果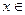 [0,1]时,总有|
[0,1]时,总有|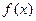 |
|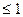 .试求
.试求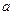 的取值范围.(3)令
的取值范围.(3)令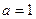 ,当
,当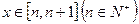 时,
时,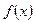 的所有整数值的个数为
的所有整数值的个数为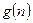 ,求证数列
,求证数列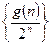 的前
的前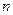 项的和
项的和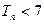 .
.(Ⅰ)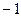 (Ⅱ)
(Ⅱ) 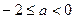 (Ⅲ)略
(Ⅲ)略
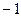 (Ⅱ)
(Ⅱ) 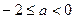 (Ⅲ)略
(Ⅲ)略解:⑴由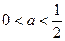 知
知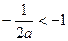 故当
故当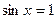 时
时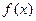 取得最大值为
取得最大值为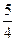 ,2分
,2分
即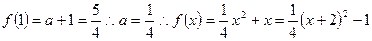 ,所以
,所以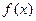 的最小值为
的最小值为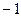 ;…4分
;…4分
⑵由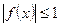 得
得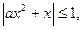
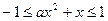 对于任意
对于任意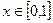 恒成立,
恒成立,
当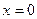 时,
时,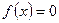 使
使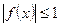 成立;……6分
成立;……6分
当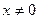 时,有
时,有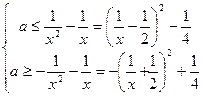 对于任意的
对于任意的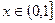 恒成立…7分
恒成立…7分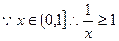 ,则
,则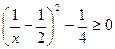 ,故要使①式成立,则有
,故要使①式成立,则有 ,又
,又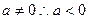 ;又
;又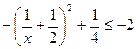 ,则有
,则有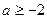 ,综上所述:
,综上所述: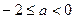 ;8分
;8分
⑶当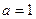 时,
时,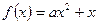 ,则此二次函数的对称轴为
,则此二次函数的对称轴为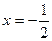 ,开口向上,故
,开口向上,故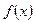 在
在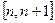 上为单调递增函数,且当
上为单调递增函数,且当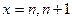 时,
时,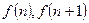 均为整数,
均为整数,
故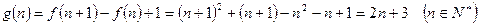 ,
,
则数列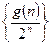 的通项公式为
的通项公式为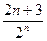 ,…10分
,…10分
故 ①,又
①,又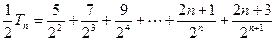 ②,
②,
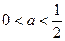 知
知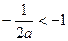 故当
故当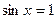 时
时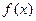 取得最大值为
取得最大值为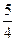 ,2分
,2分即
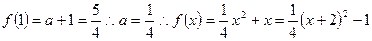 ,所以
,所以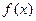 的最小值为
的最小值为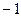 ;…4分
;…4分⑵由
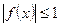 得
得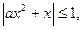
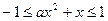 对于任意
对于任意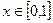 恒成立,
恒成立,当
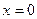 时,
时,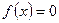 使
使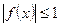 成立;……6分
成立;……6分
|
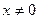 时,有
时,有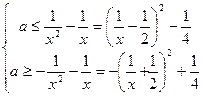 对于任意的
对于任意的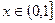 恒成立…7分
恒成立…7分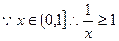 ,则
,则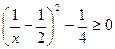 ,故要使①式成立,则有
,故要使①式成立,则有 ,又
,又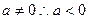 ;又
;又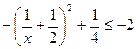 ,则有
,则有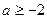 ,综上所述:
,综上所述: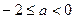 ;8分
;8分⑶当
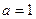 时,
时,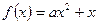 ,则此二次函数的对称轴为
,则此二次函数的对称轴为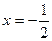 ,开口向上,故
,开口向上,故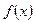 在
在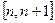 上为单调递增函数,且当
上为单调递增函数,且当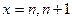 时,
时,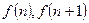 均为整数,
均为整数,故
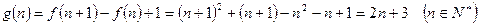 ,
,则数列
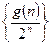 的通项公式为
的通项公式为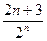 ,…10分
,…10分故
 ①,又
①,又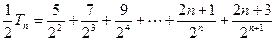 ②,
②,
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
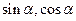 是方程
是方程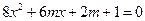 的两个实数根,求实数
的两个实数根,求实数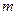 的值.
的值.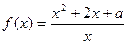
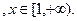 若对任意
若对任意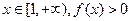 恒成立,试求实数
恒成立,试求实数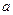 的取值范围。
的取值范围。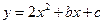 在
在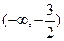 上是减函数,在
上是减函数,在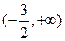 上是增函数,且两个零点
上是增函数,且两个零点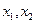 满足
满足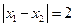 ,求二次函数的解析式。
,求二次函数的解析式。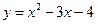 的定义域为
的定义域为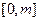 ,值域为
,值域为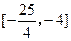 ,则
,则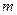 的取值范围是( )
的取值范围是( )