题目内容
(本小题满分12分）
在一个直径是50的球形器材中，嵌入一根圆轴（如图5-5），为了使圆轴不易脱出，
应该使它与球有最大的接触面积，问圆轴的半径x应是多少？
解：设圆轴的半径为x ，与球接触的圆轴的高为h ，圆轴与球的接触面积是y ．则圆轴与球的接触面积是一个圆柱的侧面积且有y=2πxh ①，其中0＜x＜25．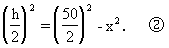
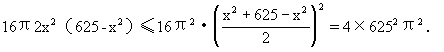
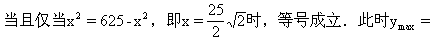
答：圆柱的半径应为
解析
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
.
相交于M、N两点，且OM⊥ON（O为坐标原点），求m；
，求直线l的方程；点P在正方体ABCD﹣A1B1C1D1的底面ABCD所在平面上，E是A1A的中点，且∠EPA=∠D1PD，则点P的轨迹是（ ）
| A．直线 | B．圆 | C．抛物线 | D．双曲线 |
已知抛物线的顶点在原点，焦点在x轴的正半轴上，若抛物线的准线与双曲线5x2－y2= 20的两条渐近线围成的三角形的面积等于
，则抛物线的方程为
| A．y2=4x | B．y2=8x | C．x2=4y | D．x2=8y |
已知抛物线
的准线与圆
相切，则
的值为
A． | B．1 | C．2 | D．4 |
（1）求圆心轨迹的参数方程
；
是
（1）中曲线
的取值范围。
本小题满分14分）
，点
是⊙
：
上任意两个不同的点，且满足
，设
为弦
的中点．
的方程；
的距离恰好等于到点
的距离？若存在，求出这样的点的坐标；若不存在，说明理由．
、
且圆心在x轴上的圆的标准方程并判断点
与圆的关系．