题目内容
(14分)在平面直角坐标系xOy中,已知圆C1:(x+3)2+(y-1)2=4和圆C2:(x
-4)2+(y-5)2=4.
(1)若点M∈⊙ C1, 点N∈⊙C2,求|MN|的取值范围;
(2)若直线l过点A(4,0),且被圆C1截得的弦长为2  ,求直线l的方程;
,求直线l的方程;
(3)设P为平面上的点,满足:存在过点P的无数多对互相垂直的直线l1和l2,它们分别与圆C1和圆C2相交,且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,试求所有满足条件的点P的坐标。
解:(1)
(2)由于直线x=4与圆C1没有交点,则直线l的斜率存在,设直线l的方程为:y=k(x-
所求直线方程为y=0,或7x+24y-28=0.
(3)设点P(a,b)满足条件,设直线l1的方程为y-b=k(x-a ),即kx-y+b-ak=0,k≠0,
),即kx-y+b-ak=0,k≠0,
则直线l2的方程为y-b=- (x-a),即x+ky-a-kb=0.根据已知条件得
(x-a),即x+ky-a-kb=0.根据已知条件得
解析

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知抛物线C: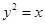 的焦点为
的焦点为 ,
, (
(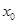 ,
, )是C上一点,
)是C上一点, =
=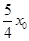 ,则
,则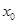 =( )
=( )
| A.1 | B.2 | C.4 | D.8 |
 ,求直线l的方程.
,求直线l的方程. 经过
经过 、
、 两点,且圆心在直线
两点,且圆心在直线 上.
上.  经过点
经过点 ,圆心M在二次曲线
,圆心M在二次曲线 上运动(1)若圆M与y轴相切,求圆M方程;(2) 已知圆M的圆心M在第一象限, 半径为
上运动(1)若圆M与y轴相切,求圆M方程;(2) 已知圆M的圆心M在第一象限, 半径为 ,动点
,动点 是圆M外一点,过点
是圆M外一点,过点 与圆M相切的切线的长为3,求动点
与圆M相切的切线的长为3,求动点 ,求
,求 的取值范围?
的取值范围? 轨迹方程
轨迹方程 应该使它与球有最大的接触面积,问圆轴的半径x应是多少?
应该使它与球有最大的接触面积,问圆轴的半径x应是多少?
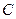 的圆心在
的圆心在
 轴的正半轴上,且圆
轴的正半轴上,且圆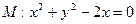 相外切,又和直线
相外切,又和直线 相切,求圆
相切,求圆 程。
程。