题目内容
点P在正方体ABCD﹣A1B1C1D1的底面ABCD所在平面上,E是A1A的中点,且∠EPA=∠D1PD,则点P的轨迹是( )
| A.直线 | B.圆 | C.抛物线 | D.双曲线 |
B
解析试题分析:由已知得 即
即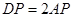 ,在平面ABCD内以AD所在直线为x轴,AD中点为坐标原点建立直角坐标系,设A(1,0),B(-1,0),P(x,y),由
,在平面ABCD内以AD所在直线为x轴,AD中点为坐标原点建立直角坐标系,设A(1,0),B(-1,0),P(x,y),由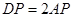 建立等式化简得轨迹方程为
建立等式化简得轨迹方程为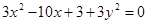 ,是圆的一般方程,所以答案选B。
,是圆的一般方程,所以答案选B。
考点:1.直角三角形中的三角函数定义;2.轨迹方程的求解

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(本小题12分)
已知椭圆C的左右焦点坐标分别是(-1,0),(1, 0),离心率
0),离心率 ,直线
,直线 与椭圆C交于不同的两点M,N,以线段MN为直径作圆P。
与椭圆C交于不同的两点M,N,以线段MN为直径作圆P。
(1)求椭圆C的方程;
(2)若圆P恰过坐标原点,求圆P的方程;
已知抛物线C: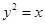 的焦点为
的焦点为 ,
, (
(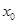 ,
, )是C上一点,
)是C上一点, =
=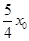 ,则
,则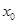 =( )
=( )
| A.1 | B.2 | C.4 | D.8 |
已知双曲线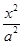 -
- =1(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( )
=1(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( )
A. - - =1 =1 | B. - - =1 =1 |
C. - - =1 =1 | D. - - =1 =1 |
 经过
经过 、
、 两点,且圆心在直线
两点,且圆心在直线 上.
上.  经过点
经过点 应该使它与球有最大的接触面积,问圆轴的半径x应是多少?
应该使它与球有最大的接触面积,问圆轴的半径x应是多少?
 于P,Q两点,现将坐标平面沿直线y= -x折成直二面角,则折后PQ长度的最小值等于
于P,Q两点,现将坐标平面沿直线y= -x折成直二面角,则折后PQ长度的最小值等于


 B.1 C.
B.1 C. D.
D.