题目内容
已知数列{an}的前n项和为Sn,a1=1,Sn=2an+1,则Sn等于( )
| A.2n-1 | B.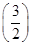 n-1 n-1 | C.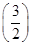 n-1 n-1 | D.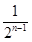 |
B
法一 由Sn=2an+1=2(Sn+1-Sn)可知,
3Sn=2Sn+1,即Sn+1=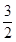 Sn,
Sn,
∴数列{Sn}是首项为S1=1,公比为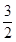 的等比数列,
的等比数列,
∴Sn=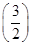 n-1.故选B.
n-1.故选B.
法二 由Sn=2an+1 ①可知a2=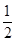 S1=
S1=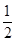 ,
,
当n≥2时,Sn-1=2an, ②
∴①-②并化简得an+1=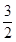 an(n≥2),
an(n≥2),
即{an}从第二项起是首项为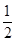 ,公比为
,公比为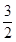 的等比数列,
的等比数列,
∴Sn=a1+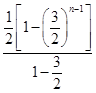 =1+
=1+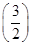 n-1-1=
n-1-1=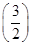 n-1(n≥2),当n=1时,满足上式.
n-1(n≥2),当n=1时,满足上式.
故选B.
法三 特殊值法,由Sn=2an+1及a1=1,
可得a2=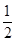 S1=
S1=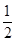 ,
,
∴当n=2时,S2=a1+a2=1+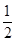 =
=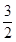 ,观察四个选项得B正确.故选B.
,观察四个选项得B正确.故选B.
3Sn=2Sn+1,即Sn+1=
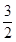 Sn,
Sn,∴数列{Sn}是首项为S1=1,公比为
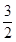 的等比数列,
的等比数列,∴Sn=
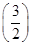 n-1.故选B.
n-1.故选B.法二 由Sn=2an+1 ①可知a2=
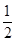 S1=
S1=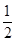 ,
,当n≥2时,Sn-1=2an, ②
∴①-②并化简得an+1=
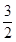 an(n≥2),
an(n≥2),即{an}从第二项起是首项为
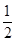 ,公比为
,公比为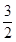 的等比数列,
的等比数列,∴Sn=a1+
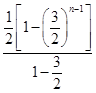 =1+
=1+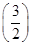 n-1-1=
n-1-1=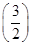 n-1(n≥2),当n=1时,满足上式.
n-1(n≥2),当n=1时,满足上式.故选B.
法三 特殊值法,由Sn=2an+1及a1=1,
可得a2=
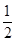 S1=
S1=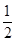 ,
,∴当n=2时,S2=a1+a2=1+
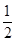 =
=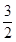 ,观察四个选项得B正确.故选B.
,观察四个选项得B正确.故选B.
练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
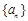 各项都是正数,
各项都是正数, ,
,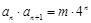 ,
,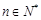 .
.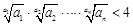 .
.
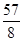
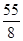
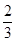 的等比数列{an}的前n项和为Sn,则( )
的等比数列{an}的前n项和为Sn,则( )