题目内容
对正整数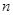 ,设抛物线
,设抛物线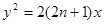 ,过
,过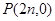 任作直线
任作直线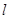 交抛物线于
交抛物线于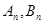 两点,则数列
两点,则数列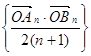 的前
的前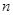 项和公式是××××× .
项和公式是××××× .
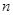 ,设抛物线
,设抛物线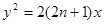 ,过
,过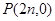 任作直线
任作直线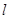 交抛物线于
交抛物线于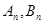 两点,则数列
两点,则数列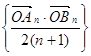 的前
的前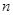 项和公式是××××× .
项和公式是××××× .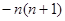
分析:设An(xn1,yn1),B(xn2,yn2),直线方程为x=ty+2n,代入抛物线方程得y2-2(2n+1)ty-4n(2n+1)=0,求出
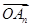 ?
? 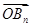 的表达式,然后利用韦达定理代入得
的表达式,然后利用韦达定理代入得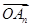 ?
? 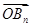 =-4n2-4n,故可得
=-4n2-4n,故可得 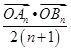 =-2n,据此可得数列
=-2n,据此可得数列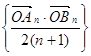 的前n项和.
的前n项和.解:设直线方程为x=ty+2n,代入抛物线方程得y2-2(2n+1)ty-4n(2n+1)=0,
设An(xn1,yn1),B(xn2,yn2),
则
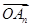 ?
? 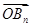 =xn1xn2+yn1yn2=(t2+1)yn1yn2+2nt(yn1+yn2)+4n2,
=xn1xn2+yn1yn2=(t2+1)yn1yn2+2nt(yn1+yn2)+4n2,用韦达定理代入得
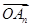 ?
? 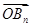 =-4n(2n+1)(t2+1)+4n(2n+1)t2+4n2=-4n2-4n,
=-4n(2n+1)(t2+1)+4n(2n+1)t2+4n2=-4n2-4n,故
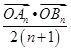 =-2n,
=-2n,故数列
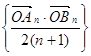 的前n项和-n(n+1),
的前n项和-n(n+1),故答案为-n(n+1).

练习册系列答案
相关题目
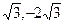 ),
),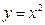 上求一点P,使过点P的切线和直线3x-y+1=0的夹角为
上求一点P,使过点P的切线和直线3x-y+1=0的夹角为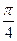 。
。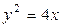 上有两个定点A、B分别在对称轴的上、下两侧,F为抛物线的焦点,并且|F
上有两个定点A、B分别在对称轴的上、下两侧,F为抛物线的焦点,并且|F A|=2,|FB|=5,
A|=2,|FB|=5, 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则p的值为 ( )
的右焦点重合,则p的值为 ( )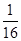


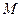 到定点
到定点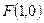 的距离与到定直线
的距离与到定直线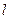 :
: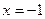 的距离相等,点C在直线
的距离相等,点C在直线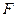 ,且法向量
,且法向量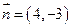 的直线与(1)中的轨迹相交于
的直线与(1)中的轨迹相交于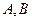 两点且点
两点且点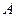 在
在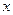 轴的上方。判断
轴的上方。判断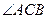 能否为钝角并说明理由。进一步研究
能否为钝角并说明理由。进一步研究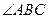 为钝角时点
为钝角时点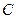 纵坐标的取值范围。
纵坐标的取值范围。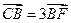 ,则直线l的斜率为___________.
,则直线l的斜率为___________. ,则抛物线的焦点坐标为________
,则抛物线的焦点坐标为________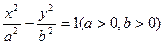 的两个焦点,M为双曲线上的点,若
的两个焦点,M为双曲线上的点,若