题目内容
【题目】设f（x）=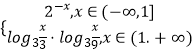 
（1）求f（log2 
）的值；
（2）求f（x）的最小值．
【答案】
（1）解：∵log2 
＜log22=1，
∴f（log2 ）= 
= 
= 
（2）解：①当x≤1时，
f（x）=2﹣x在（﹣∞，1]上是减函数，
故f（x）≥f（1）= 
；
②当x＞1时，
f（x）= 
log3 
=（log3x﹣1）（log3x﹣2）
=（log3x﹣1.5）2﹣ 
，
故当log3x=1.5时，f（x）有最小值﹣ ；
综上所述，f（x）的最小值为﹣
【解析】（1）可判断出log2 ＜1，从而代入分段函数求函数的值，（2）在分段函数的两部分分别求函数的最小值，从而求分段函数的最小值即可．
【考点精析】关于本题考查的函数的最值及其几何意义和函数的值，需要了解利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值；函数值的求法：①配方法(二次或四次)；②“判别式法”；③反函数法；④换元法；⑤不等式法；⑥函数的单调性法才能得出正确答案．
练习册系列答案
相关题目
