题目内容
定义域为R的函数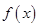 满足
满足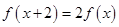 ,当
,当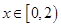 时,
时,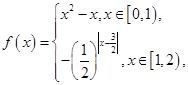 则当
则当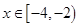 时,函数
时,函数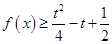 恒成立,则实数
恒成立,则实数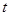 的取值范围为( )
的取值范围为( )
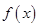 满足
满足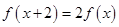 ,当
,当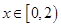 时,
时,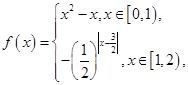 则当
则当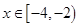 时,函数
时,函数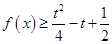 恒成立,则实数
恒成立,则实数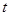 的取值范围为( )
的取值范围为( ) A. | B.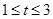 | C.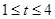 | D.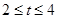 |
B
试题分析:解:当x∈[0,1)时,f(x)=x2-x∈[-
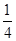 ,0],当x∈[1,2)时,f(x)=-(0.5)|x-1.5|∈[-1,-
,0],当x∈[1,2)时,f(x)=-(0.5)|x-1.5|∈[-1,-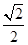 ],∴当x∈[0,2)时,f(x)的最小值为-1,又∵函数f(x)满足f(x+2)=2f(x),当x∈[-2,0)时,f(x)的最小值为-
],∴当x∈[0,2)时,f(x)的最小值为-1,又∵函数f(x)满足f(x+2)=2f(x),当x∈[-2,0)时,f(x)的最小值为-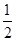 ,当x∈[-4,-2)时,f(x)的最小值为-
,当x∈[-4,-2)时,f(x)的最小值为-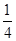 ,若x∈[-4,-2]时,f(x)≥
,若x∈[-4,-2]时,f(x)≥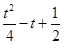
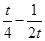 -恒成立,∴
-恒成立,∴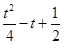 ≤-
≤-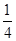 ,解得:t∈[1,3],故选B
,解得:t∈[1,3],故选B点评:本题考查的知识点是函数恒成立问题,函数的最值,分式不等式的解法,高次不等式的解法,是函数、不等式的综合应用,难度较大.

练习册系列答案
相关题目
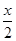 -2sin x的图象大致是( )
-2sin x的图象大致是( )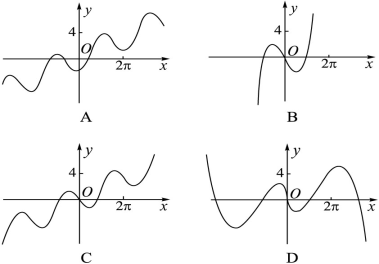
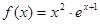 ,
,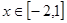 的最大值为
的最大值为 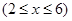 .
.
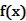 满足
满足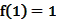 ,且
,且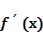 在R上恒有
在R上恒有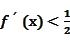 ,则不等式
,则不等式 的解集为 _______________
的解集为 _______________