题目内容
【题目】随着网络的发展,人们可以在网络上购物、玩游戏、聊天、导航等,所以人们对上网流量的需求越来越大.某电信运营商推出一款新的“流量包”套餐.为了调查不同年龄的人是否愿意选择此款“流量包”套餐,随机抽取50个用户,按年龄分组进行访谈,统计结果如右表.
组 号 | 年龄 | 访谈 人数 | 愿意 使用 |
1 | [18,28) | 4 | 4 |
2 | [28,38) | 9 | 9 |
3 | [38,48) | 16 | 15 |
4 | [48,58) | 15 | 12 |
5 | [58,68) | 6 | 2 |
(Ⅰ)若在第2、3、4组愿意选择此款“流量包”套餐的人中,用分层抽样的方法抽取12人,则各组应分别抽取多少人?
(Ⅱ)若从第5组的被调查者访谈人中随机选取2人进行追踪调查,求2人中至少有1人愿意选择此款“流量包”套餐的概率.
(Ⅲ)按以上统计数据填写下面2×2列联表,并判断以48岁为分界点,能否在犯错误不超过1%的前提下认为,是否愿意选择此款“流量包”套餐与人的年龄有关?
年龄不低于48岁的人数 | 年龄低于48岁的人数 | 合计 | |
愿意使用的人数 | |||
不愿意使用的人数 | |||
合计 |
参考公式:![]() ,其中:n=a+b+c+d.
,其中:n=a+b+c+d.
P(k2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】(Ⅰ)3人,5人,4人;(Ⅱ)![]() ;(Ⅲ)见解析.
;(Ⅲ)见解析.
【解析】试题分析:
(1)由分层抽样的定义可得分层抽样的方法抽取12人,各组分别为3人,5人,4人.
(2)列出所有可能的事件,由古典概型公式可得这2人中至少有1人愿意选择此款“流量包”套餐的概率![]() .
.
(3)结合列联表可得![]() ,则在犯错误不超过1%的前提下可以认为,是否愿意选择此款“流量包”套餐与人的年龄有关.
,则在犯错误不超过1%的前提下可以认为,是否愿意选择此款“流量包”套餐与人的年龄有关.
试题解析:
(Ⅰ)因为![]() ,
,![]() ,
,![]() ,所以第2、3、4组愿意选择此款“流量包”套餐的人中,用分层抽样的方法抽取12人,各组分别为3人,5人,4人.
,所以第2、3、4组愿意选择此款“流量包”套餐的人中,用分层抽样的方法抽取12人,各组分别为3人,5人,4人.
(Ⅱ)第5组的6人中,不愿意选择此款“流量包”套餐的4人分别记作:A、B、C、D,愿意选择此款“流量包”套餐2人分别记作x、y.则从6人中选取2人有:AB,AC,AD,Ax,Ay,BC,BD,Bx,By,CD,Cx,Cy,Dx,Dy,xy共15个结果,其中至少有1人愿意选择此款“流量包”:Ax,Ay,Bx,By,Cx,Cy,Dx,Dy,xy
共9个结果,所以这2人中至少有1人愿意选择此款“流量包”套餐的概率![]() .
.
(Ⅲ)2×2列联表:
年龄不低于48岁的人数 | 年龄低于48岁的人数 | 合计 | |
愿意使用的人数 | 14 | 28 | 42 |
不愿意使用的人数 | 7 | 1 | 8 |
合计 | 21 | 29 | 50 |
∴![]() ,
,
∴在犯错误不超过1%的前提下可以认为,是否愿意选择此款“流量包”套餐与人的年龄有关.

【题目】(本小题满分12分) 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过![]() ):
):
空气质量指数 |
|
|
|
|
|
|
空气质量等级 |
|
|
|
|
|
|
该社团将该校区在![]() 年
年![]() 天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
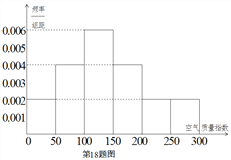
(Ⅰ)请估算![]() 年(以
年(以![]() 天计算)全年空气质量优良的天数(未满一天按一天计算);
天计算)全年空气质量优良的天数(未满一天按一天计算);
(Ⅱ)该校![]() 年
年![]() 月
月![]() 、
、![]() 日将作为高考考场,若这两天中某天出现
日将作为高考考场,若这两天中某天出现![]() 级重度污染,需要净化空气费用
级重度污染,需要净化空气费用![]() 元,出现
元,出现![]() 级严重污染,需要净化空气费用
级严重污染,需要净化空气费用![]() 元,记这两天净化空气总费用为
元,记这两天净化空气总费用为![]() 元,求
元,求![]() 的分布列及数学期望.
的分布列及数学期望.
