题目内容
9.为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加,现有来自甲协会的运动员3名,其中种子选手2名,乙协会的运动员5名,其中种子选手3名,从这8名运动员中随机选择4人参加比赛.(Ⅰ)设A为事件“选出的4人中恰有2名种子选手,且这2名种子选手来自同一个协会”,求事件A发生的概率;
(Ⅱ)设X为选出的4人中种子选手的人数,求随机变量X的分布列和数学期望.
分析 (Ⅰ)利用组合知识求出基本事件总数及事件A发生的个数,然后利用古典概型概率计算公式得答案;
(Ⅱ)随机变量X的所有可能取值为1,2,3,4,由古典概型概率计算公式求得概率,列出分布列,代入期望公式求期望.
解答 解:(Ⅰ)由已知,有P(A)=$\frac{{C}_{2}^{2}{C}_{3}^{2}+{C}_{3}^{2}{C}_{3}^{2}}{{C}_{8}^{4}}=\frac{6}{35}$,
∴事件A发生的概率为$\frac{6}{35}$;
(Ⅱ)随机变量X的所有可能取值为1,2,3,4.
P(X=k)=$\frac{{C}_{5}^{k}{C}_{3}^{4-k}}{{C}_{8}^{4}}$(k=1,2,3,4).
∴随机变量X的分布列为:
| X | 1 | 2 | 3 | 4 |
| P | $\frac{1}{14}$ | $\frac{3}{7}$ | $\frac{3}{7}$ | $\frac{1}{14}$ |
点评 本题主要考查古典概型及其概率计算公式,互斥事件、离散型随机变量的分布列与数学期望等基础知识,考查运用概率知识解决简单实际问题的能力,是中档题.

练习册系列答案
相关题目
18.某几何体的三视图如图所示,则该几何体的体积为( )
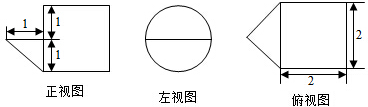

| A. | $\frac{1}{3}+2π$ | B. | $\frac{13π}{6}$ | C. | $\frac{7π}{3}$ | D. | $\frac{5π}{2}$ |
19.若(1+i)+(2-3i)=a+bi(a,b∈R,i是虚数单位),则a,b的值分别等于( )
| A. | 3,-2 | B. | 3,2 | C. | 3,-3 | D. | -1,4 |
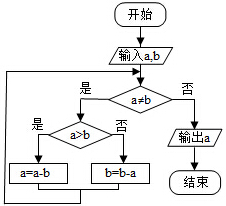 程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为14,18,则输出的a=( )
程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为14,18,则输出的a=( )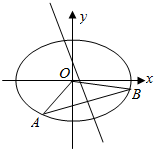 已知椭圆$\frac{x^2}{2}+{y^2}=1$上两个不同的点A,B关于直线y=mx+$\frac{1}{2}$对称.
已知椭圆$\frac{x^2}{2}+{y^2}=1$上两个不同的点A,B关于直线y=mx+$\frac{1}{2}$对称.