Question

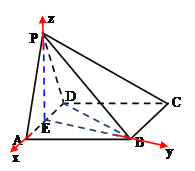
【题目】如图，四棱锥P-ABCD中，底面为菱形，且， ．

（Ⅰ）求证： ；

（Ⅱ）若，求二面角的余弦值。

Answer 1

【答案】（1）证明见解析；（2）．

【解析】试题（1）取的中点，利用菱形和等边三角形的三线合一得到线线垂直，进而得到线面垂直和线线垂直；（2）先利用勾股定理和线面垂直的判定定理得到线面垂直，建立空间直角坐标系，利用空间向量进行求解．

试题解析：（Ⅰ）证明：取的中点，连接．

∵，四边形为菱形，且，

∴和为两个全等的等边三角形，

则

∴平面，又平面，

∴；

（Ⅱ）解：在中，由已知得， ， ，

则，∴，

即，又，∴平面；

以点E为坐标原点，分别以EA，EB，EP所在直线为x，y，z轴，建立如图所示空间直角坐标系，

则E（0，0，0），C（－2， ，0），D（－1，0，0），P（0，0， ），

则＝（1，0， ），＝（－1， ，0），

由题意可设平面的一个法向量为；

设平面的一个法向量为，

由已知得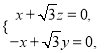： 令y＝1，则，z＝－1，

∴；

则，所以 ，

由题意知二面角的平面角为钝角，

所以二面角的余弦值为