题目内容
(本题满分12分)
椭圆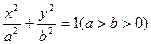 的左、右焦点分别为F1、F2,离心率
的左、右焦点分别为F1、F2,离心率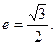 右准线为
右准线为 M、N是
M、N是 上的两个点,
上的两个点,
(1)若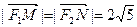 ,求椭圆方程;
,求椭圆方程;
(2)证明,当|MN|取最小值时,向量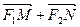 与
与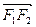 共线.
共线.
椭圆
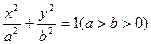 的左、右焦点分别为F1、F2,离心率
的左、右焦点分别为F1、F2,离心率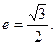 右准线为
右准线为 M、N是
M、N是 上的两个点,
上的两个点,
(1)若
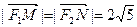 ,求椭圆方程;
,求椭圆方程;(2)证明,当|MN|取最小值时,向量
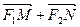 与
与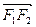 共线.
共线.解:由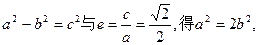
于是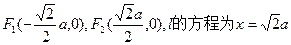
…………2分
设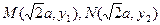 ,
,
则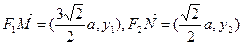
由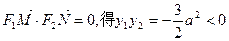 ① …………3分
① …………3分
(1)由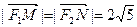 ,得
,得
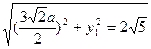 ②
②
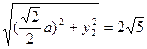 ③
③
由①,②,③三式,消去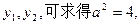 …………5分
…………5分
故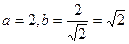
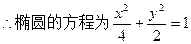 …………6分
…………6分
(2)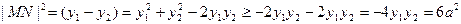
当且仅当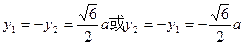 时 …………8分
时 …………8分
|MN|取得最小值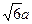 …………10分
…………10分
此时,
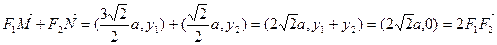
…………11分
故向量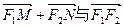 共线 …………12分
共线 …………12分
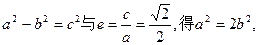
于是
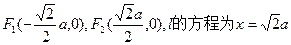
…………2分
设
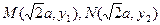 ,
,则
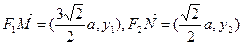
由
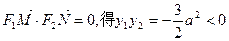 ① …………3分
① …………3分(1)由
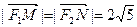 ,得
,得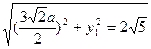 ②
②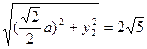 ③
③由①,②,③三式,消去
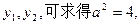 …………5分
…………5分故
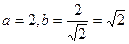
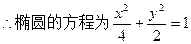 …………6分
…………6分(2)
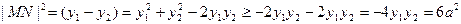
当且仅当
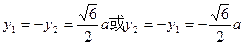 时 …………8分
时 …………8分|MN|取得最小值
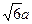 …………10分
…………10分此时,
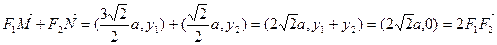
…………11分
故向量
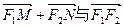 共线 …………12分
共线 …………12分略

练习册系列答案
相关题目
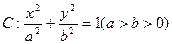 的离心率是
的离心率是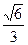 ,长轴长是为6,
,长轴长是为6,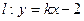 与
与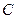 交于
交于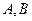 两点,已知点
两点,已知点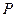 的坐标为
的坐标为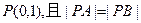 ,求直线
,求直线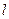 的方程。
的方程。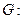
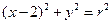 是椭圆
是椭圆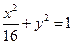 的内接△
的内接△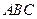 的内切圆, 其中
的内切圆, 其中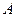 为椭圆的左顶点.
为椭圆的左顶点.
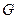 的半径
的半径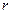 ;
; 2)过点
2)过点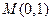 作圆
作圆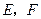 两点,
两点,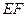 与圆
与圆 ,长轴长为
,长轴长为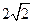 ,离心率
,离心率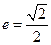 ,过右焦点
,过右焦点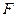 的直线
的直线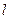 交椭圆于
交椭圆于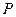 ,
,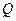 两点.
两点.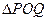 的面积;
的面积;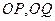 为邻边的平行四边形是矩形,求满足该条件的直线
为邻边的平行四边形是矩形,求满足该条件的直线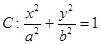 的左焦点作直线
的左焦点作直线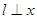 轴,交椭圆C于A,B两点,若△OAB(O为坐标原点)是直角三角形,则椭圆C的离心率e为( )
轴,交椭圆C于A,B两点,若△OAB(O为坐标原点)是直角三角形,则椭圆C的离心率e为( )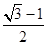
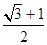
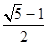
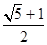
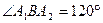 ,则椭圆的离心率为
,则椭圆的离心率为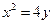 及椭圆
及椭圆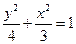 的实线部分上运动,且AB∥Y轴,则
的实线部分上运动,且AB∥Y轴,则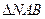 的周长的取值范围是( )
的周长的取值范围是( )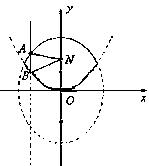
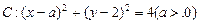 及直线l:x-y+3=O,当直线l被圆C截得的
及直线l:x-y+3=O,当直线l被圆C截得的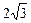 时,则a=( )
时,则a=( )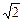
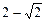
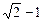
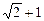
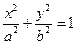 (a>b>0)的
(a>b>0)的 离心率为
离心率为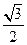 ,过右焦点F且斜率为k(k>0)的直线与椭圆C相交于A、B两点,若
,过右焦点F且斜率为k(k>0)的直线与椭圆C相交于A、B两点,若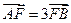 。则
。则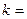 ( )
( ) 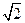 (D)
(D)