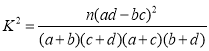题目内容
【题目】动点![]() 与定点
与定点![]() 的距离和该动点到直线
的距离和该动点到直线![]() 的距离的比是常数
的距离的比是常数![]() .
.
(1)求动点![]() 轨迹方程
轨迹方程![]() ;
;
(2)已知点![]() ,问在
,问在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得过
,使得过![]() 点的任一条斜率不为0的弦交曲线
点的任一条斜率不为0的弦交曲线![]() 于
于![]() 两点,都有
两点,都有![]() .
.
【答案】(1)![]() ;(2)存在,坐标为
;(2)存在,坐标为![]()
【解析】
(1)根据题意列出点![]() 满足的关系式,再化简方程即可.
满足的关系式,再化简方程即可.
(2) 设![]() ,再讨论当
,再讨论当![]() ⊥
⊥![]() 轴时可得
轴时可得![]() ,即若存在定点,则定点坐标为
,即若存在定点,则定点坐标为![]() .再讨论斜率存在时,设
.再讨论斜率存在时,设![]() 的方程为
的方程为![]() ,联立椭圆方程,求出韦达定理,证明
,联立椭圆方程,求出韦达定理,证明![]() 即可.
即可.
(1)由题意,知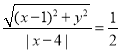 ,即
,即![]() .
.
解得曲线![]() 的方程为
的方程为![]() .
.
(2)法一:设![]() ,易知
,易知![]() ,
,
①若![]() ⊥
⊥![]() 轴时,由
轴时,由![]() ,此时
,此时![]() ,满足椭圆方程
,满足椭圆方程![]() ,
,
∴![]() ,解得
,解得![]() (舍),可知若存在定点,则定点坐标为
(舍),可知若存在定点,则定点坐标为![]() .
.
②当直线![]() 斜率存在时,设斜率为k,
斜率存在时,设斜率为k,![]()
设![]() 的方程为
的方程为![]() ,联立椭圆方程
,联立椭圆方程![]() ,
,
消去![]() 得
得![]() ,∴
,∴ .
.
![]() ,∴
,∴![]()
![]()
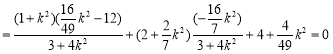 ,
,
综合①②可知,存在点![]() ,使得
,使得![]() .
.
(2)(解法二)设![]() ,易知
,易知![]() ,设
,设![]() .
.
若![]() 不垂直
不垂直![]() 轴,
轴,![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
即是![]() ①,
①,
由![]() ,得
,得![]() ,
,
![]() 代入①式得
代入①式得
![]() 化简,
化简,
整理得![]() ②,
②,
为使![]() 与斜率
与斜率![]() 无关,由②式得出
无关,由②式得出![]() ,解得
,解得![]() (舍),
(舍),
这说明![]() 与
与![]() 轴不垂直时,
轴不垂直时,![]() 是过
是过![]() 的弦,恒有
的弦,恒有![]() ,
,
若![]() ⊥
⊥![]() 轴时,
轴时,![]() :
:![]() ,
,![]() 是等腰三角形,
是等腰三角形,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
可见![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,
综上,过![]() 的弦
的弦![]() 总有
总有![]() .
.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】按照水果市场的需要等因素,水果种植户把某种成熟后的水果按其直径![]() 的大小分为不同等级.某商家计划从该种植户那里购进一批这种水果销售.为了了解这种水果的质量等级情况,现随机抽取了100个这种水果,统计得到如下直径分布表(单位:mm):
的大小分为不同等级.某商家计划从该种植户那里购进一批这种水果销售.为了了解这种水果的质量等级情况,现随机抽取了100个这种水果,统计得到如下直径分布表(单位:mm):
d |
|
|
|
|
|
等级 | 三级品 | 二级品 | 一级品 | 特级品 | 特级品 |
频数 | 1 | m | 29 | n | 7 |
用分层抽样的方法从其中的一级品和特级品共抽取6个,其中一级品2个.
(1)估计这批水果中特级品的比例;
(2)已知样本中这批水果不按等级混装的话20个约1斤,该种植户有20000斤这种水果待售,商家提出两种收购方案:
方案A:以6.5元/斤收购;
方案B:以级别分装收购,每袋20个,特级品8元/袋,一级品5元/袋,二级品4元/袋,三级品3元/袋.
用样本的频率分布估计总体分布,问哪个方案种植户的收益更高?并说明理由.
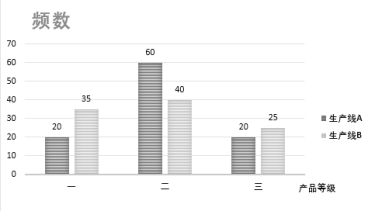
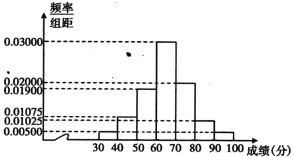
【题目】某中学共有1000人,其中男生700人,女生300人,为了了解该校学生每周平均体育锻炼时间的情况以及经常进行体育锻炼的学生是否与性别有关(经常进行体育锻炼是指:周平均体育锻炼时间不少于4小时),现在用分层抽样的方法从中收集200位学生每周平均体育锻炼时间的样本数据(单位:小时),其频率分布直方图如图.已知在样本数据中,有40位女生的每周平均体育锻炼时间超过4小时,根据独立性检验原理( )
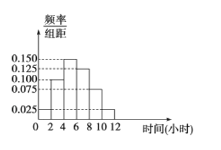
附: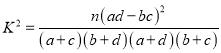 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
A.有95%的把握认为“该校学生每周平均体育锻炼时间与性别无关”
B.有90%的把握认为“该校学生每周平均体育锻炼时间与性别有关”
C.有90%的把握认为“该校学生每周平均体育锻炼时间与性别无关”
D.有95%的把握认为“该校学生每周平均体育锻炼时间与性别有关”
【题目】某省从2021年开始,高考采用取消文理分科,实行“![]() ”的模式,其中的“1”表示每位学生必须从物理、历史中选择一个科目且只能选择一个科目.某校高一年级有2000名学生(其中女生900人).该校为了解高一年级学生对“1”的选课情况,采用分层抽样的方法抽取了200名学生进行问卷调查,下表是根据调查结果得到的
”的模式,其中的“1”表示每位学生必须从物理、历史中选择一个科目且只能选择一个科目.某校高一年级有2000名学生(其中女生900人).该校为了解高一年级学生对“1”的选课情况,采用分层抽样的方法抽取了200名学生进行问卷调查,下表是根据调查结果得到的![]() 列联表.
列联表.
性别 | 选择物理 | 选择历史 | 总计 |
男生 | ________ | 50 |
|
女生 | 30 | ________ |
|
总计 | ________ | ________ | 200 |
(1)求![]() ,
,![]() 的值;
的值;
(2)请你依据该列联表判断是否有99.5%的把握认为选择科目与性别有关?说明你的理由.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001/span> |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附: ,其中
,其中![]() .
.
【题目】(在花卉进行硬枝扦插过程中,常需要用生根粉调节植物根系生长.现有20株使用了生根粉的花卉,在对最终“花卉存活”和“花卉死亡”进行统计的同时,也对在使用生根粉2个小时后的生根量进行了统计,这20株花卉生根量如下表所示,其中生根量在6根以下的视为“不足量”,大于等于6根为“足量”.现对该20株花卉样本进行统计,其中“花卉存活”的13株.已知“花卉存活”但生根量“不足量”的植株共1株.
编号 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
生根量 | 6 | 8 | 3 | 8 | 9 | 5 | 6 | 6 | 2 | 7 | 7 | 5 | 9 | 6 | 7 | 8 | 8 | 4 | 6 | 9 |
(1)完成![]() 列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为“花卉的存活”与“生根足量”有关?
列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为“花卉的存活”与“生根足量”有关?
生根足量 | 生根不足量 | 总计 | |
花卉存活 | |||
花卉死亡 | |||
总计 | 20 |
(2)若在该样本“生根不足量”的植株中随机抽取3株,求这3株中恰有1株“花卉存活”的概率.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
独立性检验中的 ,其中
,其中![]() .
.