Question

【题目】已知在直角坐标系xOy中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，圆锥曲线C的极坐标方程为p2= ，定点A（0，﹣ ），F1 ， F2是圆锥曲线C的左、右焦点，直线l经过点F1且平行于直线AF2 ．
（1）求圆锥曲线C的直角坐标方程和直线l的参数方程；
（2）若直线l与圆锥曲线C交于M，N两点，求|F1M||F1N|．

Answer 1

【答案】
（1）解：∵p2= ，∴3ρ2+ρ2sin2θ=12．

∴曲线C的直角坐标方程为3x2+3y2+y2=12，即 ．

∴F1（﹣1，0），F2（1，0），

∴直线AF2的斜率 = = ．∴直线l的倾斜角为 ．

在l上任取一点P，设有向线段F1P的长为t，

则直线l的参数方程为 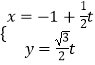（t为参数）．

（2）解：将l的参数方程代入曲线的直角坐标方程得 ，即5t2﹣4t﹣12=0．

设M，N对应的参数分别为t1，t2，则t1t2=﹣ ．

∴|F1M||F1N|=|t1||t2|=|t1t2|=

【解析】（1）根据极坐标与直角坐标的对应关系得出曲线C的直角坐标方程，根据焦点坐标计算直线l的倾斜角，令F1到直线l上一点P的有向线段t为参数写出l的参数方程；，（2）将直线l的参数方程代入曲线的直角坐标方程，得出关于t的方程，利用参数得几何意义计算|F1M||F1N|．