题目内容
已知函数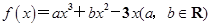 在点
在点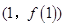 处的切线方程为
处的切线方程为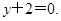
(1)求函数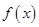 的解析式;
的解析式;
(2)若对于区间[-2,2]上任意两个自变量的值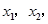 都有
都有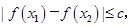 求实数c的最小值.
求实数c的最小值.
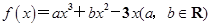 在点
在点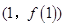 处的切线方程为
处的切线方程为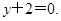
(1)求函数
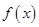 的解析式;
的解析式;(2)若对于区间[-2,2]上任意两个自变量的值
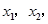 都有
都有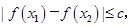 求实数c的最小值.
求实数c的最小值.(1) f(x)=x3-3x. (2) c的最小值为4.
试题分析:(1)f′(x)=3ax2+2bx-3.
根据题意,得

即
 解得
解得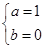
所以f(x)=x3-3x.
(2)令f′(x)=0,即3x2-3=0,得x=±1.
| x | -2 | (-2,-1) | -1 | (-1,1) | 1 | (1,2) | 2 |
| f′(x) | | + | | - | | + | |
| f(x) | -2 |  ? ? | 极大值 |  ? ? | 极小值 |  ? ? | 2 |
所以当x∈[-2,2]时,f(x)max=2,f(x)min=-2.
( 需列表格或者说明单调性,否则扣2分)
则对于区间[-2,2]上任意两个自变量的值x1,x2,都有|f(x1)-f(x2)|≤|f(x)max-f(x)min|=4,
所以c≥4.即c的最小值为4.
点评:典型题,本题属于导数应用中的基本问题,首先利用待定系数法,求得函数解析式,为进一步解题奠定了基础。利用“表解法”写出函数单调性、极值,直观明了。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
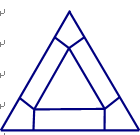
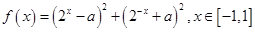 .关于
.关于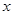 的方程
的方程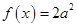 有解,则实数
有解,则实数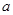 的取值范围是 _____ .
的取值范围是 _____ .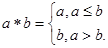 如
如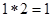 ,则函数
,则函数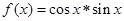 的值域为( )
的值域为( )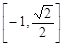
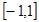

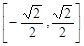
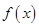 是定义在
是定义在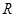 上的函数,且
上的函数,且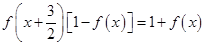 ,
,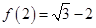 ,则
,则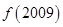 值为( )
值为( )
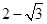
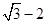
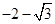
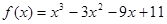
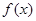 的递减区间;
的递减区间;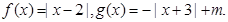
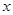 的不等式
的不等式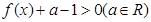 ;
;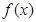 的图象恒在函数
的图象恒在函数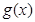 图象的上方(没有公共点),求
图象的上方(没有公共点),求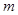 的取值范围。
的取值范围。
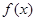 在
在 上为增函数,求正实数
上为增函数,求正实数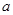 的取值范围;
的取值范围; 时,求
时,求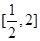 上的最大值和最小值;
上的最大值和最小值;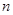 ,都有
,都有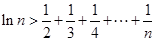 。
。