题目内容
(本小题满分12分)
已知函数
(1)若函数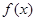 在
在 上为增函数,求正实数
上为增函数,求正实数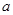 的取值范围;
的取值范围;
(2)当 时,求
时,求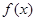 在
在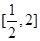 上的最大值和最小值;
上的最大值和最小值;
(3) 当 时,求证:对大于1的任意正整数
时,求证:对大于1的任意正整数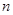 ,都有
,都有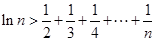 。
。
已知函数

(1)若函数
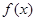 在
在 上为增函数,求正实数
上为增函数,求正实数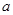 的取值范围;
的取值范围;(2)当
 时,求
时,求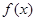 在
在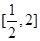 上的最大值和最小值;
上的最大值和最小值;(3) 当
 时,求证:对大于1的任意正整数
时,求证:对大于1的任意正整数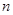 ,都有
,都有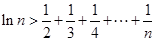 。
。(1)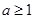 (2)最大值为
(2)最大值为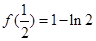 ,最小值为
,最小值为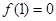 (3)
(3)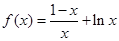 ,
,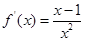
函数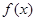 在
在 上为增函数,当
上为增函数,当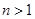 时,令
时,令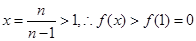
 即
即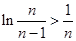 所以
所以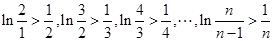
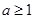 (2)最大值为
(2)最大值为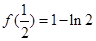 ,最小值为
,最小值为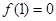 (3)
(3)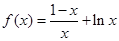 ,
,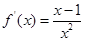
函数
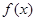 在
在 上为增函数,当
上为增函数,当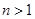 时,令
时,令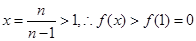
 即
即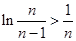 所以
所以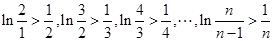
试题分析:(1)
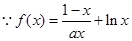 ,
,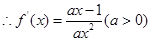
 函数
函数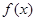 在
在 上为增函数,
上为增函数, 对任意的
对任意的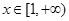 恒成立,
恒成立, 对任意的
对任意的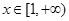 恒成立,即
恒成立,即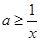 任意的
任意的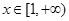 恒成立,…………2分
恒成立,…………2分而当
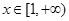 时,
时,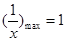 ,
,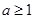 ……………………4分
……………………4分(2)当
 时,
时,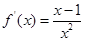
当
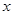 变化时,
变化时,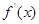 ,
,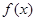 的变化情况如下表
的变化情况如下表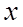 | 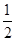 |  | 1 |  | 2 |
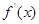 | | 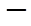 | 0 | 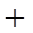 | |
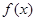 | 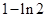 |  | 0 | 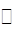 | 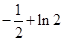 |
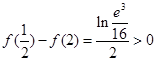
所以
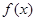 在区间
在区间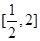 上的最大值为
上的最大值为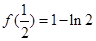 ,最小值为
,最小值为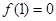 …………8分
…………8分(3)当
 时,
时,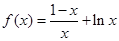 ,
,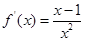 ,
,所以函数
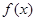 在
在 上为增函数
上为增函数当
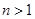 时,令
时,令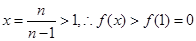
 即
即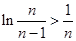 ……………………10分
……………………10分所以
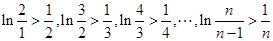
所以
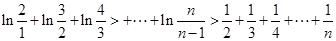
即对大于1的任意正整数
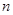 ,都有
,都有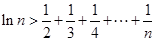 。…………12分
。…………12分点评:导数主要用于判定函数单调性,求最值,证明不等式恒成立,其中证明不等式或已知不等式恒成立求参数问题常转化为求函数最值问题

练习册系列答案
相关题目
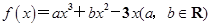 在点
在点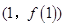 处的切线方程为
处的切线方程为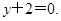
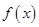 的解析式;
的解析式;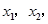 都有
都有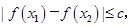 求实数c的最小值.
求实数c的最小值.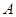 、
、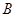 两个项目,预计投资
两个项目,预计投资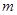 万元可获得利润
万元可获得利润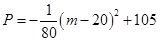
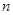 万元可获得利润
万元可获得利润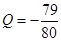
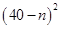
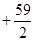
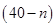 万元.若该企业用40
万元.若该企业用40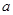 元(一年定期),若年利率为
元(一年定期),若年利率为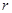 保持不变,且每年到期存款和利息自动转为新的一年定期,到2012年底将所有存款及利息全部取回,则可取回的钱数(元)为
保持不变,且每年到期存款和利息自动转为新的一年定期,到2012年底将所有存款及利息全部取回,则可取回的钱数(元)为

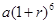
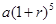
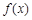 在
在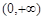 上是单调递增函数,当
上是单调递增函数,当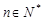 时,
时,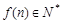 ,且
,且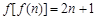 ,则( )
,则( )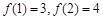
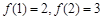
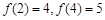

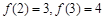
 :
: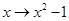 的条件下,象3的原象是( )
的条件下,象3的原象是( ) 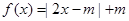 .
.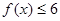 的解集为
的解集为 ,求实数
,求实数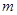 的值;
的值;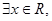 使
使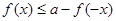 能成立,求实数a的取值范围.
能成立,求实数a的取值范围.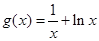 ,
,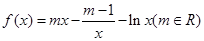 .
.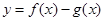 在
在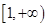 上为单调函数,求m的取值范围;
上为单调函数,求m的取值范围;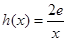 ,若在
,若在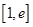 上至少存在一个
上至少存在一个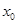 ,使得
,使得 成立,求
成立,求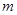 的取值范围.
的取值范围.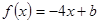 ,且不等式
,且不等式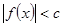 的解集为
的解集为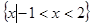 ,
,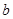 的值;
的值; 的不等式
的不等式