题目内容
已知函数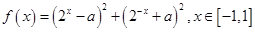 .关于
.关于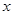 的方程
的方程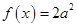 有解,则实数
有解,则实数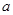 的取值范围是 _____ .
的取值范围是 _____ .
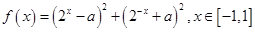 .关于
.关于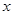 的方程
的方程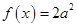 有解,则实数
有解,则实数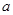 的取值范围是 _____ .
的取值范围是 _____ .
试题分析:
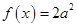 即
即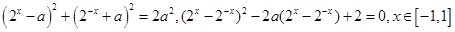 ,令t=
,令t=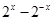 ,则
,则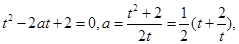
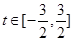 ,由“对号函数”的性质得,实数
,由“对号函数”的性质得,实数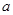 的取值范围是
的取值范围是 。
。点评:简单题,涉及函数方程问题,往往可借助于奇偶性等研究函数图象,分析方程有解的情况。本题利用“分离参数法”,转化成求函数值域问题。

练习册系列答案
相关题目
题目内容
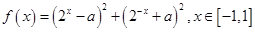 .关于
.关于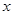 的方程
的方程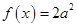 有解,则实数
有解,则实数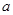 的取值范围是 _____ .
的取值范围是 _____ .
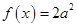 即
即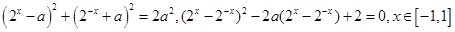 ,令t=
,令t=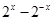 ,则
,则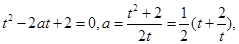
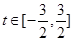 ,由“对号函数”的性质得,实数
,由“对号函数”的性质得,实数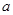 的取值范围是
的取值范围是 。
。