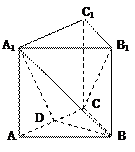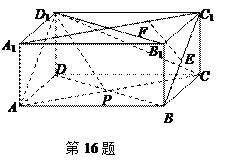题目内容
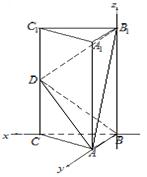
(本题满分12分) 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,2AB=2BC=CC1=2,D是棱CC1的中点 (1)求证B1D⊥平面ABD;









 (2)平面AB1D与侧面BB1C1C所成锐角的大小 C1 B1
(2)平面AB1D与侧面BB1C1C所成锐角的大小 C1 B1











 (2)平面AB1D与侧面BB1C1C所成锐角的大小 C1 B1
(2)平面AB1D与侧面BB1C1C所成锐角的大小 C1 B1 (Ⅰ)略 (Ⅱ) 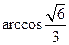
方法一:(1)在 中,
中,
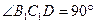 ,
,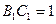 ,
,
∴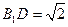 ,同理
,同理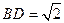
在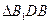 中,∵
中,∵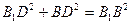 ∴
∴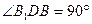
即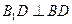 又∵在直三棱柱
又∵在直三棱柱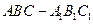 中,
中,
∴ 平面
平面 , 而
, 而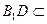 平面
平面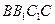 ,∴
,∴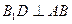
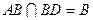 ∴
∴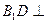 平面
平面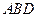 ; 6分
; 6分
(2)由(1)知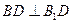 ,
,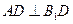 ,平面
,平面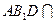 平面
平面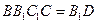
∴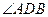 就是平面
就是平面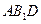 与侧面
与侧面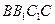 所成角的平面角
所成角的平面角
在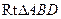 中,
中,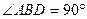 ,
,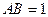 ,
,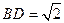
∴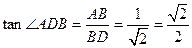 ,∴
,∴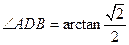 .
.
即平面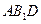 与侧面
与侧面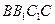 所成锐角的大小为
所成锐角的大小为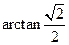 . …12分
. …12分
方法二:
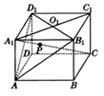
如图所示建立空间直角坐标系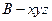 则
则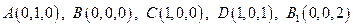 ,
,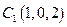 于是
于是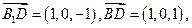
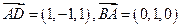
(1)∵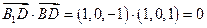 ,
,
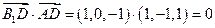 ∴
∴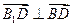 ,
,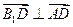 ,即
,即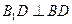 ,
,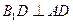 ,又
,又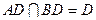 ∴
∴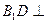 平面
平面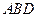 ;…6分
;…6分
(2)设平面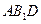 的法向量为
的法向量为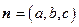 ,则由
,则由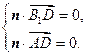 得
得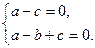
令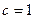 得
得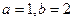 ∴
∴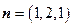 ,易知平面
,易知平面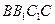 的法向量为
的法向量为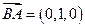 ,
,
设平面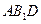 与平面
与平面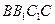 所成角的大小为
所成角的大小为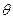 ,则
,则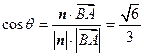 .
.
即平面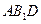 与侧面
与侧面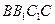 所成锐角的大小为
所成锐角的大小为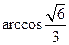 . …12分
. …12分
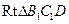 中,
中,
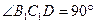 ,
,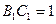 ,
,
∴
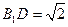 ,同理
,同理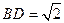
在
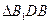 中,∵
中,∵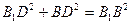 ∴
∴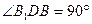
即
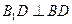 又∵在直三棱柱
又∵在直三棱柱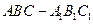 中,
中,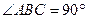
∴
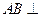 平面
平面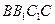 , 而
, 而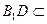 平面
平面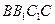 ,∴
,∴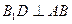
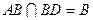 ∴
∴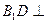 平面
平面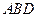 ; 6分
; 6分(2)由(1)知
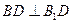 ,
,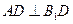 ,平面
,平面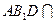 平面
平面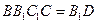
∴
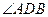 就是平面
就是平面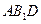 与侧面
与侧面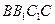 所成角的平面角
所成角的平面角在
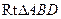 中,
中,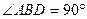 ,
,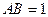 ,
,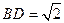
∴
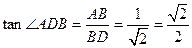 ,∴
,∴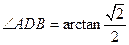 .
.即平面
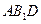 与侧面
与侧面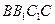 所成锐角的大小为
所成锐角的大小为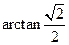 . …12分
. …12分方法二:
如图所示建立空间直角坐标系
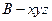 则
则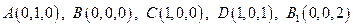 ,
,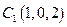 于是
于是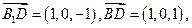
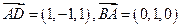
(1)∵
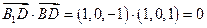 ,
,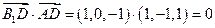 ∴
∴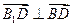 ,
,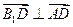 ,即
,即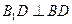 ,
,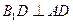 ,又
,又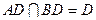 ∴
∴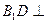 平面
平面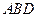 ;…6分
;…6分(2)设平面
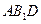 的法向量为
的法向量为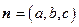 ,则由
,则由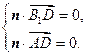 得
得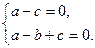
令
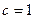 得
得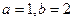 ∴
∴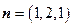 ,易知平面
,易知平面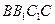 的法向量为
的法向量为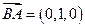 ,
,设平面
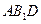 与平面
与平面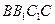 所成角的大小为
所成角的大小为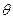 ,则
,则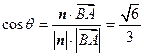 .
.即平面
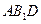 与侧面
与侧面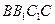 所成锐角的大小为
所成锐角的大小为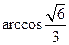 . …12分
. …12分
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
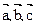 ,若
,若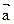 ∥
∥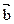 ,
,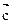 则
则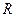 的球互相外切,且每个球都同时与另两个半径为
的球互相外切,且每个球都同时与另两个半径为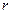 的球外切.如果这两个半径为
的球外切.如果这两个半径为