题目内容
(本小题满分13分)若集合 具有以下性质:①
具有以下性质:① ②若
②若 ,则
,则 ,且
,且 时,
时, .则称集合
.则称集合 是“好集”.
是“好集”.
(Ⅰ)分别判断集合 ,有理数集Q是否是“好集”,并说明理由;
,有理数集Q是否是“好集”,并说明理由;
(Ⅱ)设集合 是“好集”,求证:若
是“好集”,求证:若 ,则
,则 ;
;
(Ⅲ)对任意的一个“好集”A,分别判断下面命题的真假,并说明理由.
命题 :若
:若 ,则必有
,则必有 ;
;
命题 :若
:若 ,且
,且 ,则必有
,则必有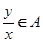 ;
;
 具有以下性质:①
具有以下性质:① ②若
②若 ,则
,则 ,且
,且 时,
时, .则称集合
.则称集合 是“好集”.
是“好集”.(Ⅰ)分别判断集合
 ,有理数集Q是否是“好集”,并说明理由;
,有理数集Q是否是“好集”,并说明理由;(Ⅱ)设集合
 是“好集”,求证:若
是“好集”,求证:若 ,则
,则 ;
;(Ⅲ)对任意的一个“好集”A,分别判断下面命题的真假,并说明理由.
命题
 :若
:若 ,则必有
,则必有 ;
;命题
 :若
:若 ,且
,且 ,则必有
,则必有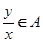 ;
;(Ⅰ)有理数集 是“好集”. (Ⅱ)
是“好集”. (Ⅱ)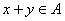 .
.
(Ⅲ)命题 均为真命题..
均为真命题..
 是“好集”. (Ⅱ)
是“好集”. (Ⅱ)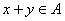 .
. (Ⅲ)命题
 均为真命题..
均为真命题.. (I)先假设集合 是“好集”.因为
是“好集”.因为 ,
, ,所以
,所以
这与 矛盾.这样就确定集合
矛盾.这样就确定集合 不是“好集”.有理数Q也采用同样的方法,进行推证.
不是“好集”.有理数Q也采用同样的方法,进行推证.
(II)根据好集的定义 是“好集”,则
是“好集”,则 ,然后再根据x,y的任意性,可证明
,然后再根据x,y的任意性,可证明 .
.
(III)本小题也是先假设p、q都是真命题,然后根据好集的定义进行推证..
(Ⅰ)集合 不是“好集”. 理由是:假设集合
不是“好集”. 理由是:假设集合 是“好集”.
是“好集”.
因为 ,
, ,所以
,所以 . 这与
. 这与 矛盾.…………2分
矛盾.…………2分
有理数集 是“好集”. 因为
是“好集”. 因为 ,
, ,对任意的
,对任意的 ,有
,有 ,且
,且 时,
时, .所以有理数集
.所以有理数集 是“好集”. ………………………………4分
是“好集”. ………………………………4分
(Ⅱ)因为集合 是“好集”,所以
是“好集”,所以  .若
.若 ,则
,则 ,即
,即 .
.
所以 ,即
,即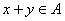 . …………………………6分
. …………………………6分
(Ⅲ)命题 均为真命题. 理由如下: ………………………………………7分
均为真命题. 理由如下: ………………………………………7分
对任意一个“好集” ,任取
,任取 , 若
, 若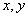 中有0或1时,显然
中有0或1时,显然 .
.
下设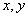 均不为0,1. 由定义可知:
均不为0,1. 由定义可知: .所以
.所以 ,即
,即 .
.
所以 . 由(Ⅱ)可得:
. 由(Ⅱ)可得: ,即
,即 . 同理可得
. 同理可得 .
.
若 或
或 ,则显然
,则显然 .若
.若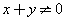 且
且 ,则
,则 .
.
所以 . 所以
. 所以  .由(Ⅱ)可得:
.由(Ⅱ)可得: .
.
所以 .综上可知,
.综上可知, ,即命题
,即命题 为真命题.若
为真命题.若 ,且
,且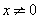 ,则
,则 .
.
所以 ,即命题
,即命题 为真命题. ……………………………………13分
为真命题. ……………………………………13分
 是“好集”.因为
是“好集”.因为 ,
, ,所以
,所以
这与
 矛盾.这样就确定集合
矛盾.这样就确定集合 不是“好集”.有理数Q也采用同样的方法,进行推证.
不是“好集”.有理数Q也采用同样的方法,进行推证.(II)根据好集的定义
 是“好集”,则
是“好集”,则 ,然后再根据x,y的任意性,可证明
,然后再根据x,y的任意性,可证明 .
.(III)本小题也是先假设p、q都是真命题,然后根据好集的定义进行推证..
(Ⅰ)集合
 不是“好集”. 理由是:假设集合
不是“好集”. 理由是:假设集合 是“好集”.
是“好集”. 因为
 ,
, ,所以
,所以 . 这与
. 这与 矛盾.…………2分
矛盾.…………2分有理数集
 是“好集”. 因为
是“好集”. 因为 ,
, ,对任意的
,对任意的 ,有
,有 ,且
,且 时,
时, .所以有理数集
.所以有理数集 是“好集”. ………………………………4分
是“好集”. ………………………………4分(Ⅱ)因为集合
 是“好集”,所以
是“好集”,所以  .若
.若 ,则
,则 ,即
,即 .
.所以
 ,即
,即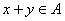 . …………………………6分
. …………………………6分(Ⅲ)命题
 均为真命题. 理由如下: ………………………………………7分
均为真命题. 理由如下: ………………………………………7分对任意一个“好集”
 ,任取
,任取 , 若
, 若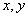 中有0或1时,显然
中有0或1时,显然 .
.下设
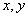 均不为0,1. 由定义可知:
均不为0,1. 由定义可知: .所以
.所以 ,即
,即 .
. 所以
 . 由(Ⅱ)可得:
. 由(Ⅱ)可得: ,即
,即 . 同理可得
. 同理可得 .
.若
 或
或 ,则显然
,则显然 .若
.若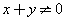 且
且 ,则
,则 .
.所以
 . 所以
. 所以  .由(Ⅱ)可得:
.由(Ⅱ)可得: .
.所以
 .综上可知,
.综上可知, ,即命题
,即命题 为真命题.若
为真命题.若 ,且
,且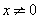 ,则
,则 .
.所以
 ,即命题
,即命题 为真命题. ……………………………………13分
为真命题. ……………………………………13分 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ②
② ③
③ ④0
④0 ⑤0
⑤0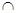

 其中错误写法的个数为 ( )
其中错误写法的个数为 ( ) ,则集合
,则集合 的子集个数是( )
的子集个数是( ) 关于运算
关于运算 满足:
满足: ,都有
,都有 ;
; ,使得对一切
,使得对一切 ,都有
,都有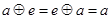 ,则称
,则称
 ① ②
① ②
 ④
④  ⑤
⑤ 中有三个元素,那么
中有三个元素,那么 的取值范围为 ____
的取值范围为 ____ M则m= , n= .
M则m= , n= . 为两个非空集合,定义集合
为两个非空集合,定义集合 ,若
,若 ,
, ,则
,则 中的元素个数是
中的元素个数是 若
若 ,则
,则 为_____.
为_____. ,则
,则



