题目内容

18．求函数f（x）=$\frac{x}{{x}^{2}+3}$（x＞0）的最大值以及取得最大值时x的值．

分析 变形可得f（x）=$\frac{1}{x+\frac{3}{x}}$，由基本不等式可得x+$\frac{3}{x}$的最小值，进而可得原式的最大值．

解答 解：化简可得f（x）=$\frac{x}{{x}^{2}+3}$=$\frac{1}{x+\frac{3}{x}}$，
∵x+$\frac{3}{x}$≥2$\sqrt{x•\frac{3}{x}}$=2$\sqrt{3}$，
当且仅当x=$\frac{3}{x}$即x=$\sqrt{3}$时上式取最小值2$\sqrt{3}$，
∴当x=$\sqrt{3}$时f（x）取最大值$\frac{1}{2\sqrt{3}}$=$\frac{\sqrt{3}}{6}$．

点评 本题考查基本不等式求最值，变形为可用基本不等式的形式是解决问题的关键，属基础题．

练习册系列答案
相关题目
8．已知数列{an}满足a1=2，an+1=an+n则a3-a1=3，数列{an}的通项公式为$\frac{{n}^{2}-n+4}{2}$．
9．已知数列{an}，{bn}中，a1=1，bn=（1-$\frac{{{a}_{n}}^{2}}{{{a}_{n+1}}^{2}}$）•$\frac{1}{{a}_{n+1}}$，n∈N*，数列{bn}的前n项和Sn．
（1）若an=2n-1，求Sn；
（2）是否存在等比数列{an}使bn+2=Sn对任意n∈N*恒成立？若存在，求出所有满足条件的数列{an}的通项公式；若不存在，说明理由．
6．已知向量$\vec a$=（cos（-x+$\frac{π}{3}$），1），$\vec b$=（3，-2），f（x）=$\vec a$•$\vec b$
（1）求函数f（x）的单调减区间；
（2）若函数f（x）的图象上各点纵坐标不变，横坐标缩短为原来的$\frac{1}{2}$得到函数g（x）的图象，试求函数y=g（x）在[0，$\frac{π}{2}}$]的值域．
13．已知a、b、c均为正数，若a+b+c，b+c-a，c+a-b，a+b-c依次成等比数列，且公比为q，则q3+q2+q的值为（　　）
A．0B．1C．3D．不能确定
3．若关于x的不等式ax2+ax+1＞0（a≠0）恒成立，则$\frac{9}{a}$+a的最小值为6．
10．Sn是数列{an}的前n项和，
（1）若an+1=an+an-1（n≥2），且a7=8，求S10；
（2）an=$\frac{1}{3}$（2n-（-1）n），bn=anan+1，bn-Sn•h＞0对任意正整数n都成立，求h的范围．
7．下列说法中正确的是（　　）
A．若a＞b，则$\sqrt{a}$＞$\sqrt{b}$B．若|a|＞b，则a2＞b2C．若a＞b，则a2＞b2D．若a＞|b|，则a2＞b2
8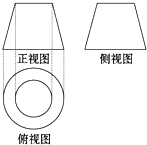．如图是一个几何体的三视图，其中正视图和侧视图都是一个两底长分别为2和4，腰长为4的等腰梯形，则该几何体的侧面积是（　　）
A．6πB．12πC．18πD．24π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网