题目内容
20.为了得到函数y=sin(2x-$\frac{π}{4}$)的图象,只要将函数y=sin(x-$\frac{π}{4}$)上所有的点( )| A. | 横坐标伸长到原来的2倍,纵坐标不变 | |
| B. | 横坐标缩短到原来的$\frac{1}{2}$倍,纵坐标不变 | |
| C. | 纵坐标伸长到原来的2倍,横坐标不变 | |
| D. | 纵坐标缩短到原来的$\frac{1}{2}$倍,横坐标不变 |
分析 由条件根据函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:将函数$y=sin(x-\frac{π}{4})$上所有的点横坐标缩短到原来的$\frac{1}{2}$倍,纵坐标不变,可得函数$y=sin(2x-\frac{π}{4})$的图象,
故选:B.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
8.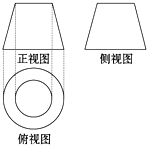 如图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )
如图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )
 如图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )
如图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )| A. | 6π | B. | 12π | C. | 18π | D. | 24π |
15.化简:$cos(\frac{5π}{2}-α)$=( )
| A. | sinα | B. | -sinα | C. | cosα | D. | -cosα |
12.函数f(x)=$\frac{\sqrt{x}}{x-1}$的定义域是( )
| A. | [0,+∞) | B. | [0,1)∪(1,+∞) | C. | (0,1) | D. | (0,1)∪(1,+∞) |
9.如图是一个空间几何体的三视图,则该几何体的全面积为( )
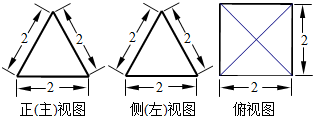

| A. | 12 | B. | 16 | C. | $\frac{{4\sqrt{3}}}{3}$+4 | D. | 4$\sqrt{3}$+4 |
10.设f(x)是定义在R上的偶函数,对任意x∈R,都有f(x-1)=f(x+1),且当x∈[0,1]时,f(x)=1-3x,若在区间[-6,6]内关于x的方程f(x)-loga(x+3)=0(0<a<1)恰有5个不同的实数根,则a的取值范围是( )
| A. | $(\frac{{\sqrt{6}}}{6},\frac{1}{2})$ | B. | $(\frac{{\sqrt{6}}}{6},1)$ | C. | $(\frac{1}{2},1)$ | D. | $(\frac{1}{2},+∞)$ |