题目内容
10.若sin6α+cos6α=$\frac{1}{4}$,求cos2015α的值.分析 由同角三角函数间的基本关系得到sin2α+cos2α=1,变形后代入已知等式代入求出cosα的值,确定出α的度数,代入原式计算即可得到结果.
解答 解:∵sin2α+cos2α=1,∴sin2α=1-cos2α,
∴sin6α+cos6α=(sin2α)3+cos6α=$\frac{1}{4}$,
把sin2α=1-cos2α代入得:(1-cos2α)3+cos6α=$\frac{1}{4}$,
整理得:(2cos2α-1)2=0,
∴2cos2α-1=0,即cos2α=$\frac{1}{2}$,
∴cosα=$\frac{\sqrt{2}}{2}$,即α=$\frac{π}{4}$,
则cos2015α=cos$\frac{2015π}{4}$=cos(504π-$\frac{π}{4}$)=cos(-$\frac{π}{4}$)=cos$\frac{π}{4}$=$\frac{\sqrt{2}}{2}$.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
20.图是一算法的程序框图,若输出结果为S=5040,则在判断框中应填入的条件是( )
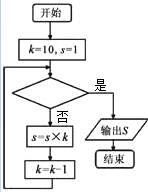

| A. | k≤9 | B. | k≤8 | C. | k≤7 | D. | k≤6 |
1.若$a={3^{0.4}},b={log_π}3,c={log_3}sin\frac{3}{π}$,则( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | b>c>a |
18.设M(x0,y0)为抛物线C:x2=4y上一点,F为抛物线C的焦点,以F为圆心、|FM|为半径的圆和抛物线C的准线相交,则y0的取值范围是( )
| A. | (0,1) | B. | [0,1] | C. | (1,+∞) | D. | [1,+∞) |
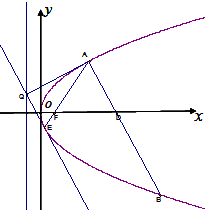 已知抛物线C顶点为O(0,0),焦点为F(1,0),A为C上异于顶点的任意一点,过点A的直线l交C 于另一点B,交x轴的正半轴于点D,且有|FA|=|FD|,延长AF交曲线C于点E.过点E作直线l1平行于l,设l1与此抛物线准线交于点Q.
已知抛物线C顶点为O(0,0),焦点为F(1,0),A为C上异于顶点的任意一点,过点A的直线l交C 于另一点B,交x轴的正半轴于点D,且有|FA|=|FD|,延长AF交曲线C于点E.过点E作直线l1平行于l,设l1与此抛物线准线交于点Q.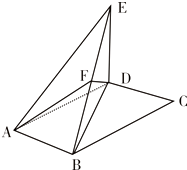 如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4,将△CBD沿 BD折起到△EBD的位置,使平面EBD⊥平面ABD
如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4,将△CBD沿 BD折起到△EBD的位置,使平面EBD⊥平面ABD