��Ŀ����
15�� ��֪������C����ΪO��0��0��������ΪF��1��0����AΪC�����ڶ��������һ�㣬����A��ֱ��l��C ����һ��B����x����������ڵ�D������|FA|=|FD|���ӳ�AF������C�ڵ�E������E��ֱ��l1ƽ����l����l1����������߽��ڵ�Q��
��֪������C����ΪO��0��0��������ΪF��1��0����AΪC�����ڶ��������һ�㣬����A��ֱ��l��C ����һ��B����x����������ڵ�D������|FA|=|FD|���ӳ�AF������C�ڵ�E������E��ֱ��l1ƽ����l����l1����������߽��ڵ�Q�������������ߵ�C�ķ��̣�
�������A��B��E��������ֱ�ΪyA��yB��yE����$\frac{{{y_A}-{y_B}}}{{{y_A}-{y_E}}}$��ֵ��
�������AEQ�������Сֵ��
���� ������������C����ΪO��0��0��������ΪF��1��0�����ɵ������߿������ң����ɵõ������߷��̣�
��������ͨ��$A��\frac{t^2}{4}��t��$���õ�D�����꣬�Ӷ��õ�ֱ��AD�ķ��̣����yB��ͨ��ֱ��AE�ķ������yE�������������$\frac{{{y_A}-{y_B}}}{{{y_A}-{y_E}}}$��ֵ��
�������AEQ�������ֵ�������������ı���ʽS��AQE=$\frac{1}{2}$|QG|•|yA-yE|�������������þ�ֵ����ʽ����Сֵ��
��� �⣺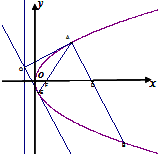 ������������C����ΪO��0��0��������ΪF��1��0����
������������C����ΪO��0��0��������ΪF��1��0����
���������ߵķ���Ϊy2=4x��
������$A��\frac{t^2}{4}��t��$��$|{AF}|=\frac{t^2}{4}+1$��
��|AF|=|DF|��${x_D}-1=\frac{t^2}{4}+1$��
��$D��\frac{t^2}{4}+2��0��$��
��ֱ��AD�ķ���Ϊ$y=-\frac{t}{2}��x-\frac{t^2}{4}-2��$��
ֱ��AE�ķ���Ϊ$y=\frac{4t}{{{t^2}-4}}��x-1��$��
��$\left\{{\begin{array}{l}{y=\frac{4t}{{{t^2}-4}}��x-1��}\\{{y^2}=4x}\end{array}}\right.$���ɵ�${y^2}-\frac{{{t^2}-4}}{t}y-4=0$
��yA=t����${y_E}=\frac{-4}{t}$��
��$\left\{{\begin{array}{l}{y=-\frac{t}{2}��x-\frac{t^2}{4}-2��}\\{{y^2}=4x}\end{array}}\right.$���ɵ�${y^2}+\frac{8}{t}y-{t^2}-8=0$
��yA=t��${y_B}=-t-\frac{8}{t}$
��$\frac{{{y_B}-{y_A}}}{{{y_E}-{y_A}}}=\frac{{-2t-\frac{8}{t}}}{{-t-\frac{4}{t}}}=2$��
����ֱ��l1����Ϊy=-$\frac{t}{2}$x-$\frac{2}{t}$��
��x=-1���ɵ�Q��-1��$\frac{t}{2}$-$\frac{2}{t}$����yE=$\frac{{y}_{A}+{y}_{B}}{2}$��ȡAB���е�G��
QG��x�ᣬ��S��AQE=$\frac{1}{2}$|QG|•|yA-yE|��
|QG|=$\frac{1}{2}$��$\frac{{t}^{2}}{4}$+$\frac{4}{{t}^{2}}$+2��=$\frac{1}{2}$��$\frac{2}{t}$+$\frac{t}{2}$��2������S��AQE=$\frac{1}{16}$��t+$\frac{4}{t}$��3��$\frac{1}{16}$•��2$\sqrt{t•\frac{4}{t}}$��3=4��
��S��AQE����СֵΪ4�����ҽ���t=��2ȡ�Ⱥţ�
���� ���⿼�������ߵķ��̺����ʵ����ã�����ֱ�߷��̵������ã��Լ�����������������������ʽ�����ã������е��⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | 2014 | B�� | 2015 | C�� | 2016 | D�� | 2017 |