题目内容
19.(1)已知向量$\overrightarrow{a}$=(-2,1),$\overrightarrow{b}$=(x,y).若x,y分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足$\overrightarrow{a}$•$\overrightarrow{b}$=-1的概率;(2)已知集合A=[-2,2],B=[-1,1],设M={(x,y)|x∈A,y∈B},在集合M内随机取出一个元素(x,y).求以(x,y)为坐标的点到直线x+y=0的距离不大于$\frac{\sqrt{2}}{2}$的概率.
分析 (1)确定基本事件的个数,即可求出满足$\overrightarrow{a}$•$\overrightarrow{b}$=-1的概率;
(2)由以(x,y)为坐标的点到直线x+y=0的距离不大于$\frac{\sqrt{2}}{2}$,求出x,y满足的关系,得到区域面积,求面积比.
解答 解:(1)将一枚质地均匀的正方体骰子先后抛掷两次,所包含的基本事件总数为6×6=36个;
由$\overrightarrow{a}$•$\overrightarrow{b}$=-1有-2x+y=-1,所以满足$\overrightarrow{a}$•$\overrightarrow{b}$=-1的基本事件为(1,1),(2,3),(3,5),共3个;
故满足$\overrightarrow{a}$•$\overrightarrow{b}$=-1的概率为$\frac{3}{36}$=$\frac{1}{12}$;
(2)由以(x,y)为坐标的点到直线x+y=0的距离不大于$\frac{\sqrt{2}}{2}$,所以$\frac{|x+y|}{\sqrt{2}}$≤$\frac{\sqrt{2}}{2}$,即|x+y|≤1,满足条件的事件是图中阴影部分,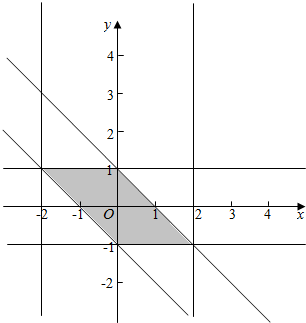
所以以(x,y)为坐标的点到直线x+y=0的距离不大于$\frac{\sqrt{2}}{2}$的概率为$\frac{1×2}{2×4}$=$\frac{1}{4}$.
点评 本题考查了古典概型、几何概型的概率求法,几何概型的概率关键是将所求的概率利用基本事件的集合度量即区域的长度或者面积或者体积表示,求比值.

练习册系列答案
相关题目
9.若sinx+siny=1,则cosx-cosy的取值范围是( )
| A. | $[-\sqrt{3},\;\;\sqrt{3}]$ | B. | $[-\sqrt{2},\;\;\sqrt{2}]$ | C. | [-1,1] | D. | [-2,2] |