题目内容
8.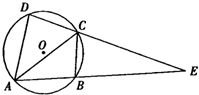 如图所示,四边形ABCD的外接圆为圆O,线段AB与线段DC的延长线交于点E,$\frac{AD}{DE}$=$\frac{1}{3}$.
如图所示,四边形ABCD的外接圆为圆O,线段AB与线段DC的延长线交于点E,$\frac{AD}{DE}$=$\frac{1}{3}$.(1)若BC=1,求BE的长度;
(2)若AC为∠DAB的角平分线,记BE=λDC(λ∈R),求λ的值.
分析 (1)运用圆的内接四边形的性质和三角形相似的判定和性质,即可求得BE=3;
(2)运用三角形的内角平分线定理和圆的切割线定理,结合条件,即可得到λ的值为3.
解答 解:(1)∵四边形ABCD的外接圆为圆O,
线段AB与线段DC的延长线交于点E,
由∠BCE=∠DAE,∠BEC=∠DEA,
∴△EBC∽△EDA,
∴$\frac{BE}{DE}=\frac{BC}{AD}$,
∵$\frac{AD}{DE}$=$\frac{1}{3}$,BC=1,
∴BE=3;
(2)在△DAE中,AC为∠DAB的角平分线,
则$\frac{AD}{AE}$=$\frac{DC}{CE}$,即有AD•CE=AE•DC①
由于EA,ED是圆的两条割线,
则DE•CE=AE•BE②
①÷②,$\frac{AD}{DE}$=$\frac{DC}{BE}$,
由$\frac{AD}{DE}$=$\frac{1}{3}$,可得$\frac{DC}{BE}$=$\frac{1}{3}$,
由BE=λDC(λ∈R),
可得λ=3.
点评 本题考查圆的内接四边形的性质,主要三角形相似的判定和性质,同时考查三角形内角平分线的性质和圆的切割线定理的运用,属于中档题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
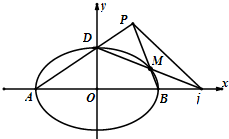 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,-2),且离心率为$\frac{{\sqrt{5}}}{3}$.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,-2),且离心率为$\frac{{\sqrt{5}}}{3}$.