题目内容
5.已知函数f(x)=ax2+bln(x+1).(1)若a=$\frac{1}{2}$,b=-2,求f(x)的单调区间;
(2)若a=$\frac{1}{2}$,讨论f(x)的单调性;
(3)若a=$\frac{1}{2}$,b=-2,求f(x)在x=0处的切线方程;
(4)若a=$\frac{1}{2}$,讨论f(x)与y=3的交点个数.
分析 (1)f′(x)=x-2(x+1)=-x-2,x>0,利用导数即可判断.
(2)f′(x)=x+b(x+1)=(1+b)x+b,x>0.分类讨论求解不等式即可.
(3)f′(0)=-2,f(0)=0,利用导数的几何意义得出:切线过(0,0),斜率为-2,再运用直线的方程求解即可.
(3)根据(2)结论得出利用单调性,可判断交点个数.
解答 解:f(x)=ax2+bln(x+1).f′(x)=2ax+b(x+1),x>0.
(1)若a=$\frac{1}{2}$,b=-2,f′(x)=x-2(x+1)=-x-2,x>0.
∵可判断f′(x)<0,在(0,+∞)恒成立,
∴f(x)在(0,+∞)单调递减.
(2)a=$\frac{1}{2}$,f′(x)=x+b(x+1)=(1+b)x+b,x>0.
∵(1+b)x+b>0,
当b>-1时,x$>-\frac{b}{1+b}$,y′>0,
x$<-\frac{b}{1+b}$,y′<0,
当b<-1时,x$<-\frac{b}{1+b}$,y′>0,x$>-\frac{b}{1+b}$,y′<0,
可判断:-1<b<0时,$-\frac{b}{1+b}$>0,f(x)在(0,$-\frac{b}{1+b}$)单调递减,在($-\frac{b}{1+b}$,+∞)单调递增.
当b≥0时,f(x)在(0,+∞)上单调递增.
当b≤-1时,(1+b)x+b<0在(0,+∞)上恒成立,故b≤-1时,f(x)在(0,+∞)上单调递减.
(3)∵a=$\frac{1}{2}$,b=-2,f′(x)=x-2(x+1)=-x-2,f(x)=$\frac{1}{2}$x2-2ln(x+1).
∴f′(0)=-2,f(0)=0,
切线过(0,0),斜率为-2,
方程为y=-2x.
(4)若a=$\frac{1}{2}$,f′(x)=x+b(x+1)=(1+b)x+b,x>0.f(x)=$\frac{1}{2}$x2+bln(x+1).f(0)=0
已知得出;-1<b<0时,$-\frac{b}{1+b}$>0,f(x)子(0,$-\frac{b}{1+b}$)单调递减,在($-\frac{b}{1+b}$,+∞)单调递增.
当b≥0时,f(x)在(0,+∞)上单调递增.
当b≤-1时,(1+b)x+b<0在(0,+∞)上恒成立,故b≤-1时,f(x)在(0,+∞)上单调递减.
∴-1<b<0时,f(x)与y=3的交点有1个.
当b≥0时,f(x)与y=3的交点有1个.
当b≤-1时,f(x)与y=3的交点有0个.
综上:b>-1,f(x)与y=3的交点有1个
当b≤-1时,f(x)与y=3的交点有0个.
点评 本题考查了函数的单调性与导数之间的关系,一个函数在其定义域内的某个区间上单调,说明函数的导函数在该区间内恒大于等于0或恒小于等于0.分类讨论的思想.此题是中档题

 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,-2),且离心率为$\frac{{\sqrt{5}}}{3}$.
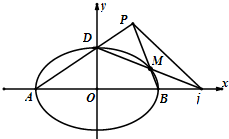
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,-2),且离心率为$\frac{{\sqrt{5}}}{3}$. 已知点p(c,$\frac{3}{2}$c)在以F(c,0)为右焦点的椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,斜率为1的直线m过点F与椭圆Γ交于A,B两点,且与直线l:x=4c交于点M.
已知点p(c,$\frac{3}{2}$c)在以F(c,0)为右焦点的椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,斜率为1的直线m过点F与椭圆Γ交于A,B两点,且与直线l:x=4c交于点M.