题目内容
15.已知空间点A(x,1,2)和点B(2,3,4),且|AB|=2$\sqrt{6}$,则点A的坐标为(6,1,2)或(-2,1,2).分析 直接利用空间距离公式求解即可.
解答 解:空间点A(x,1,2)和点B(2,3,4),且|AB|=2$\sqrt{6}$,
可得$\sqrt{{(x-2)}^{2}+{(1-3)}^{2}{+(2-4)}^{2}}$=$2\sqrt{6}$,
解得x=6或-2,
A的坐标(6,1,2)或(-2,1,2)
故答案为:(6,1,2)或(-2,1,2).
点评 本题考查空间两点间距离公式的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知函数y=f(x)是定义在R上的任意不恒为零的函数,则下列判断:①y=f(|x|)为偶函数;②y=f(x)+f(-x)为非奇非偶函数;③y=f(x)-f(-x)为奇函数;④y=[f(x)]2 为偶函数.其中正确判断的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.甲、乙、丙三人到三个景点旅游,每人只去一个景点,设事件A为“三个人去的景点不相同”,事件B为“甲独自去一个景点”,则概率P(A|B)等于( )
| A. | $\frac{4}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
4.等差数列{an}的前n项和为Sn,如果存在正整数k和l(k≠l),使得Sk=kl2,Sl=lk2,则( )
| A. | Sk+1的最小值为-6 | B. | Sk+l的最大值为-6 | ||
| C. | Sk+1的最小值为6 | D. | Sk+l的最小值为6 |
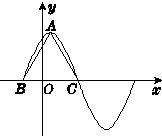 函数f(x)=3cosωx+$\sqrt{3}$sinωx(ω>0)在一个周期内的图象如图所示,A为图象的最高点.B、C为图象与x轴的交点,且△ABC为正三角形.
函数f(x)=3cosωx+$\sqrt{3}$sinωx(ω>0)在一个周期内的图象如图所示,A为图象的最高点.B、C为图象与x轴的交点,且△ABC为正三角形.