题目内容
6.在△ABC中,AB=14cm,$\frac{AD}{BD}$=$\frac{5}{9}$,DE∥BC,CD⊥AB,CD=12cm,求△ABC的面积和周长.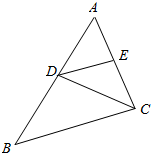
分析 由AB=14cm,CD=12cm得S△ABC=84,利用勾股定理求出BC、AC,求△ABC的周长.
解答 解:∵在△ABC中,AB=14cm,CD⊥AB,CD=12cm,
∴S△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$×14×12=84(cm2),
∵$\frac{AD}{BD}$=$\frac{5}{9}$,∴AD:AB=5:14,
∴BD=AB-AD=9cm,
∴在Rt△ACD中,AC=13(cm),
在Rt△BCD中,BC=15(cm),
∴△ABC的周长为:AB+AC+BC=42(cm).
点评 此题考查了平行线性质以及勾股定理.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.某公共汽车站每隔10分钟有一辆汽车到达,乘客到达车站的时刻是任意的,则一个乘客候车时间不超过7分钟的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{5}{10}$ | D. | $\frac{7}{10}$ |
18.若三角形两边相等,则该两边所对的内角相等,在△ABC中,AB=AC,所以在△ABC中,∠B=∠C,以上推理运用的规则是( )
| A. | 三段论推理 | B. | 假言推理 | C. | 关系推理 | D. | 完全归纳推理 |