题目内容
20.甲、乙、丙三人到三个景点旅游,每人只去一个景点,设事件A为“三个人去的景点不相同”,事件B为“甲独自去一个景点”,则概率P(A|B)等于( )| A. | $\frac{4}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
分析 这是求甲独自去一个景点的前提下,三个人去的景点不同的概率,求出相应基本事件的个数,即可得出结论.
解答 解:甲独自去一个景点,则有3个景点可选,乙丙只能在甲剩下的哪两个景点中选择,可能性为2×2=4
所以甲独自去一个景点的可能性为3×2×2=12
因为三个人去的景点不同的可能性为3×2×1=6,
所以P(A|B)=$\frac{6}{12}$=$\frac{1}{2}$.
故选:C.
点评 本题考查条件概率,考查学生的计算能力,确定基本事件的个数是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.某公共汽车站每隔10分钟有一辆汽车到达,乘客到达车站的时刻是任意的,则一个乘客候车时间不超过7分钟的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{5}{10}$ | D. | $\frac{7}{10}$ |
8.满足条件|z-i|+|z+i|=3的复数z在复平面上对应点的轨迹是( )
| A. | 一条直线 | B. | 两条直线 | C. | 圆 | D. | 椭圆 |
12.如图是函数f(x)=x3+bx2+cx+d的大致图象,则x1+x2=( )
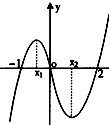

| A. | $\frac{2}{3}$ | B. | $\frac{10}{9}$ | C. | $\frac{8}{9}$ | D. | $\frac{28}{9}$ |
9.已知定义在R上的函数f(x),若f(x)是奇函数,f(x+1)是偶函数,当0≤x≤1时,f(x)=x2,则f(2015)=( )
| A. | -1 | B. | 1 | C. | 0 | D. | 20152 |