题目内容
3.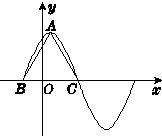 函数f(x)=3cosωx+$\sqrt{3}$sinωx(ω>0)在一个周期内的图象如图所示,A为图象的最高点.B、C为图象与x轴的交点,且△ABC为正三角形.
函数f(x)=3cosωx+$\sqrt{3}$sinωx(ω>0)在一个周期内的图象如图所示,A为图象的最高点.B、C为图象与x轴的交点,且△ABC为正三角形.(1)求ω的值及f(x)的值域;
(2)若f(x0)=$\frac{{8\sqrt{3}}}{5}$,且x0∈(-$\frac{10}{3}$,$\frac{2}{3}$),求f(x0+1)的值.
分析 (1)化简函数解析式可得f(x)=2$\sqrt{3}$sin $({ωx+\frac{π}{3}})$,由题意可求BC,由周期公式可求ω,由正弦函数的性质可求值域.
(2)由已知及(1)可求sin $({\frac{{π{x_0}}}{4}+\frac{π}{3}})$,结合范围x0∈$({-\frac{10}{3},\frac{2}{3}})$,得$\frac{{π{x_0}}}{4}$+$\frac{π}{3}$∈$({-\frac{π}{2},\frac{π}{2}})$,可求cos $({\frac{{π{x_0}}}{4}+\frac{π}{3}})$,故f(x0+1)=2$\sqrt{3}$sin $({\frac{{π{x_0}}}{4}+\frac{π}{4}+\frac{π}{3}})$=2$\sqrt{3}$sin $[{({\frac{{π{x_0}}}{4}+\frac{π}{3}})+\frac{π}{4}}]$利用两角和的正弦函数公式即可求值.
解答 解:(1)由已知可得f(x))=3cosωx+$\sqrt{3}$sinωx=2$\sqrt{3}$sin $({ωx+\frac{π}{3}})$…(2分)
易得正三角形ABC的高为2$\sqrt{3}$,则BC=4,
所以函数f(x)的周期为4×2=8,即$\frac{2π}{ω}$=8,解得ω=$\frac{π}{4}$.
所以函数f(x)的值域为[-$2\sqrt{3}$,$2\sqrt{3}$]…(6分)
(2)因为f(x0)=$\frac{{8\sqrt{3}}}{5}$,由(1)有f(x0)=2$\sqrt{3}$sin $({\frac{{π{x_0}}}{4}+\frac{π}{3}})$=$\frac{{8\sqrt{3}}}{5}$,即sin $({\frac{{π{x_0}}}{4}+\frac{π}{3}})$=$\frac{4}{5}$,
由x0∈$({-\frac{10}{3},\frac{2}{3}})$,得$\frac{{π{x_0}}}{4}$+$\frac{π}{3}$∈$({-\frac{π}{2},\frac{π}{2}})$.
即cos $({\frac{{π{x_0}}}{4}+\frac{π}{3}})$=$\sqrt{1-{{({\frac{4}{5}})}^2}}$=$\frac{3}{5}$,
故f(x0+1)=2$\sqrt{3}$sin $({\frac{{π{x_0}}}{4}+\frac{π}{4}+\frac{π}{3}})$
=2$\sqrt{3}$sin $[{({\frac{{π{x_0}}}{4}+\frac{π}{3}})+\frac{π}{4}}]$
=$2\sqrt{3}[{sin({\frac{{π{x_0}}}{4}+\frac{π}{3}})cos\frac{π}{4}+cos({\frac{{π{x_0}}}{4}+\frac{π}{3}})sin\frac{π}{4}}]$
=$2\sqrt{3}({\frac{4}{5}×\frac{{\sqrt{2}}}{2}+\frac{3}{5}×\frac{{\sqrt{2}}}{2}})$=$\frac{{7\sqrt{6}}}{5}$.…(12分)
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,三角函数的化简求值,正弦函数的图象与性质,属于基本知识的考查.

| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{5}{10}$ | D. | $\frac{7}{10}$ |
| A. | 三段论推理 | B. | 假言推理 | C. | 关系推理 | D. | 完全归纳推理 |
| A. | 一条直线 | B. | 两条直线 | C. | 圆 | D. | 椭圆 |
| A. | $\frac{2}{3}$ | B. | $\frac{10}{9}$ | C. | $\frac{8}{9}$ | D. | $\frac{28}{9}$ |