题目内容
7.若向量$\overrightarrow{a}$=(2,1)和$\overrightarrow{b}$=(x-1,y)垂直,则|$\overrightarrow{a}+\overrightarrow{b}$|的最小值为$\sqrt{5}$.分析 由已知向量垂直得到数量积为0,由此得到x,y的等式,用,x,y表示|$\overrightarrow{a}+\overrightarrow{b}$|,求最小值.
解答 解:因为向量$\overrightarrow{a}$=(2,1)和$\overrightarrow{b}$=(x-1,y)垂直,所以2x-2+y=0,
所以$\overrightarrow{a}+\overrightarrow{b}$=(x+1,y+1),|$\overrightarrow{a}+\overrightarrow{b}$|2=(x+1)2+(y+1)2,|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{(x+1)^{2}+(y+1)^{2}}$表示(-1,-1)到直线上点的距离,
所以|$\overrightarrow{a}+\overrightarrow{b}$|的最小值为$\frac{|-2-2-1|}{\sqrt{5}}=\sqrt{5}$;
故答案为:$\sqrt{5}$.
点评 本题考查了向量垂直的性质以及向量模的求法;本题利用了点到直线的距离求最小值.

练习册系列答案
相关题目
18.若三角形两边相等,则该两边所对的内角相等,在△ABC中,AB=AC,所以在△ABC中,∠B=∠C,以上推理运用的规则是( )
| A. | 三段论推理 | B. | 假言推理 | C. | 关系推理 | D. | 完全归纳推理 |
2.若2弧度的圆心角所对的弧长为4cm,则这个圆心角所夹的扇形的面积是( )
| A. | 2πcm2 | B. | 2 cm2 | C. | 4πcm2 | D. | 4 cm2 |
12.如图是函数f(x)=x3+bx2+cx+d的大致图象,则x1+x2=( )
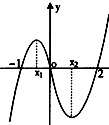

| A. | $\frac{2}{3}$ | B. | $\frac{10}{9}$ | C. | $\frac{8}{9}$ | D. | $\frac{28}{9}$ |
19.函数f(x)=$\frac{{\sqrt{16-{x^2}}}}{{|{x+5}|+|{x-4}|}}$为( )
| A. | 奇函数 | B. | 偶函数 | C. | 非奇非偶函数 | D. | 既奇又偶函数 |