题目内容
【题目】已知函数f（x）=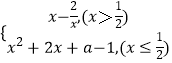 
（其中a＞0，a为常数），求函数f（x）的零点．
【答案】解：①x＞ 
时，f（x）=0，即x﹣ 
=0，解得x= 
；
②当x≤ 时，f（x）=x2+2ax+a﹣1，△=4﹣4（a﹣1）=8﹣4a，
当a＞2时，△＜0，f（x）=0无实根；
当a=2时，△=0，f（x）=0，解得x=﹣1
∵x∈（﹣∞， ]，
∴f（x）有一个零点﹣1
当0＜a＜2时，△＞0，x2+2ax+a﹣1=0，解得x=﹣1± 
，
∵﹣1﹣ ＜0＜ ，﹣1+ ＜﹣1+ ＜ ，
∴﹣1± 都是f（x）的零点．
综上所述，当a＞2时，f（x）的零点为： ；
当a=2时，f（x）的零点为： 和﹣1，
当0＜a＜2时，f（x）的零点为： 和﹣1+ ，﹣1﹣
【解析】根据分段函数和函数零点的定义，分类讨论，即可求出函数的零点．
练习册系列答案
相关题目
