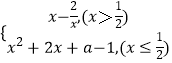题目内容
【题目】已知函数f(x)= ![]()
(1)计算f(1)+f(0)的值;
(2)计算f(x)+f(1﹣x)的值;
(3)若关于x的不等式:f[23x﹣2﹣x+m(2x﹣2﹣x)+ ![]() ]<
]< ![]() 在区间[1,2]上有解,求实数m的取值范围.
在区间[1,2]上有解,求实数m的取值范围.
【答案】
(1)解:∵f(x)= ![]()
∴f(1)+f(0)= ![]() +
+ ![]()
= ![]() +
+ ![]()
=2﹣ ![]()
=1
(2)解:f(x)+f(1﹣x)
= ![]()
= ![]() =1
=1
(3)解:∵f(x)= ![]() =
= ![]() ,
,
∴f(x)在[1,2]上单调递增,
∵f( ![]() )=
)= ![]() =
= ![]() ,
,
∴f[ ![]() ]<
]< ![]() =f(
=f( ![]() ),
),
∵f(x)在[1,2]上单调递增,
∴23x﹣2﹣x+m(2x﹣2﹣x)+ ![]() ,
,
∴23x﹣2﹣x+m(2x﹣2﹣x)<0,
∴m<﹣ ![]() =
= ![]() =﹣(22x+1),
=﹣(22x+1),
当x=1时,﹣(22x+1)max=﹣5.
∴m<﹣5.
∴实数m的取值范围(﹣∞,﹣5)
【解析】(1)根据函数的解析式直接计算f(1)+f(0)的值.(2)根据函数的解析式直接计算f(x)+f(1﹣x)的值.(3)推导出f(x)在[1,2)上单调递增,从而得到23x﹣2﹣x+m(2x﹣2﹣x)<0,由此能求出实数m的取值范围.
【考点精析】利用函数的值对题目进行判断即可得到答案,需要熟知函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法.

 名校课堂系列答案
名校课堂系列答案【题目】有甲、乙两个班级进行数学考试,按照大于或等于90分为优秀,90分以下为非优秀统计成绩后,得到如表的列联表.
优秀 | 非优秀 | 总计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 100 |
已知在全部100人中抽到随机抽取1人为优秀的概率为 ![]() .
.
(1)请完成如表的列联表;
(2)根据列联表的数据,有多大的把握认为“成绩与班级有关系“?
(3)按分层抽样的方法,从优秀学生中抽出6名组成一个样本,再从样本中抽出2名学生,求恰好有1个学生在甲班的概率.
参考公式和数据:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
下面的临界值表供参考:
p(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |