题目内容
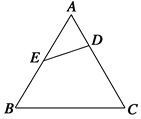
如图，在正△ABC中，点D，E分别在边BC，AC上，且BD＝
BC，CE＝CA，AD，BE相交于点P，求证：
(1)P，D，C，E四点共圆；
(2)AP⊥CP.
BC，CE＝CA，AD，BE相交于点P，求证： (1)P，D，C，E四点共圆；
(2)AP⊥CP.
（1）见解析（2）见解析
(1)在正△ABC中，由BD＝BC，
CE＝CA，可得△ABD≌△BCE，
∴∠ADB＝∠BEC，
∴∠ADC＋∠BEC＝180°，
∴P，D，C，E四点共圆．
(2)如图，连结DE，在△CDE中，CD＝2CE，∠ACD＝60°，
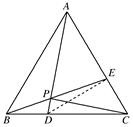
由正弦定理知∠CED＝90°，
由P，D，C，E四点共圆知，∠DPC＝∠DEC，
∴AP⊥CP.
BC，CE＝
CA，可得△ABD≌△BCE，∴∠ADB＝∠BEC，
∴∠ADC＋∠BEC＝180°，
∴P，D，C，E四点共圆．
(2)如图，连结DE，在△CDE中，CD＝2CE，∠ACD＝60°，
由正弦定理知∠CED＝90°，
由P，D，C，E四点共圆知，∠DPC＝∠DEC，
∴AP⊥CP.
练习册系列答案
相关题目
求证：
；（2）
∽
中，
，
，
，
、
为垂足，若AE=4，BE=1，则AC= .
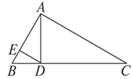
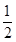BC，则sin∠MCA＝
＝
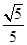
，AE＝BE，则有