题目内容
【题目】设f(x)=|ax﹣1|+|x+2|,(a>0).
(Ⅰ)若a=1,时,解不等式 f(x)≤5;
(Ⅱ)若f(x)≥2,求a的最小值.
【答案】解:(Ⅰ)若a=1,f(x)= 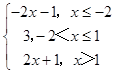 ,
,
由f(x)的单调性及f(﹣3)=f(2)=5,得f(x)≤5 的解集为{x|﹣3≤x≤2}.
(Ⅱ)f(x)= 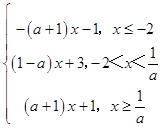 ,
,
当x∈(﹣∞,﹣2]时,f(x)单调递减;当x∈[ ![]() ,+∞)时,f(x)单调递增,
,+∞)时,f(x)单调递增,
又f(x)的图象连续不断,所以f(x)≥2,当且仅当f(﹣2)=2a+1≥2,且f( ![]() )=
)= ![]() +2≥2,
+2≥2,
求得a≥ ![]() ,故a的最小值为
,故a的最小值为 ![]()
【解析】(Ⅰ)分类讨论化简f(x)的解析式,由f(x)的单调性及f(﹣3)=f(2)=5,得f(x)≤5 的解集.(Ⅱ)由f(x)= 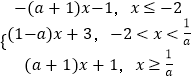 的单调性,以及f(x)的图象连续不断,可得要是f(x)≥2,当且仅当f(﹣2)≥2,且f(
的单调性,以及f(x)的图象连续不断,可得要是f(x)≥2,当且仅当f(﹣2)≥2,且f( ![]() )≥2,由此求得a的最小值.
)≥2,由此求得a的最小值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
