题目内容
【题目】已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若a,b∈[﹣1,1],a+b≠0时,有 ![]() >0成立.
>0成立.
(Ⅰ)判断f(x)在[﹣1,1]上的单调性,并证明;
(Ⅱ)解不等式:f(2x﹣1)<f(1﹣3x);
(Ⅲ)若f(x)≤m2﹣2am+1对所有的a∈[﹣1,1]恒成立,求实数m的取值范围.
【答案】解:(Ⅰ)任取x1,x2∈[﹣1,1],且x1<x2,则﹣x2∈[﹣1,1],∵f(x)为奇函数,
∴f(x1)﹣f(x2)=f(x1)+f(﹣x2)= ![]() (x1﹣x2),
(x1﹣x2),
由已知得 ![]() >0,x1﹣x2<0,∴f(x1)﹣f(x2)<0,即f(x1)<f(x2).
>0,x1﹣x2<0,∴f(x1)﹣f(x2)<0,即f(x1)<f(x2).
∴f(x)在[﹣1,1]上单调递增.
(Ⅱ)∵f(x)在[﹣1,1]上单调递增,∴ 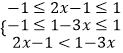
∴不等式的解集为 ![]() .
.
(Ⅲ)∵f(1)=1,f(x)在[﹣1,1]上单调递增.∴在[﹣1,1]上,f(x)≤1.
问题转化为m2﹣2am+1≥1,即m2﹣2am≥0,对a∈[﹣1,1]恒成立.
下面来求m的取值范围.设g(a)=﹣2ma+m2≥0.
①若m=0,则g(a)=0≥0,对a∈[﹣1,1]恒成立.
②若m≠0,则g(a)为a的一次函数,若g(a)≥0,对a∈[﹣1,1]恒成立,
必须g(﹣1)≥0且g(1)≥0,∴m≤﹣2或m≥2.
综上,m=0 或m≤﹣2或m≥2
【解析】1、由题意可得,根据证明函数单调性的定义。任取x1,x2∈[﹣1,1],且x1<x2,判断f(x1)﹣f(x2)的正负即得结果。
2、由题意可得f(x)在[﹣1,1]上单调递增,f(2x﹣1)<f(1﹣3x)可得, 2x-1, 1-3x![]() [﹣1,1], 2x-1>1-3x。求以上不等式的交集。
[﹣1,1], 2x-1>1-3x。求以上不等式的交集。
3、由(2)可知函数f(x)单调递增即有f(x)![]() f(1)=1故f(x)
f(1)=1故f(x)![]() 可表示为
可表示为![]() ,对a∈[﹣1,1]恒成立。令g(a)=﹣2ma+m2 , 若m=0,则g(a)=0对a∈[﹣1,1]恒成立;若m≠0,则g(a)为a的一次函数,根据函数在定义域[﹣1,1]上的最小值大于0,可求得m的取值范围。
,对a∈[﹣1,1]恒成立。令g(a)=﹣2ma+m2 , 若m=0,则g(a)=0对a∈[﹣1,1]恒成立;若m≠0,则g(a)为a的一次函数,根据函数在定义域[﹣1,1]上的最小值大于0,可求得m的取值范围。