题目内容
【题目】求适合下列条件的椭圆的标准方程：
（1）两个焦点的坐标分别是 
， 
，椭圆上一点 
到两焦点的距离之和为 
；
（2）焦点在坐标轴上，且经过 
和 
两点．
【答案】
（1）解：∵焦点在 
轴上，∴设其标准方程为 
．
∵ 
, 
，∴ 
， 
.∴ 
.
∴所求椭圆方程为 
（2）解：解法一：①当焦点在 
轴上时，设椭圆的标准方程为 
，
将 
和 
代入标准方程解得 
.
∴所求椭圆的标准方程为 
.
②当焦点在y轴上时，设椭圆的标准方程为 .
将 和 代入标准方程解得 
.
，不合题意，舍去．
综上，所求椭圆的标准方程为 .
解法二：设所求椭圆方程为 
且 
，
依题意，得 
解得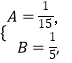 
∴所求椭圆的标准方程为
【解析】（1）根据椭圆的坐标可知焦点在y轴上且可确定c的值，由椭圆定义可知
+
=2a可求出a，再根据a2=b2+c2可求出b；（2）依题意可设椭圆的方程为Ax2+By2=1（A
，B且A≠B），将点A、B的坐标分别代入，联立组成方程组即可求出A，B的值.
练习册系列答案
相关题目
