题目内容
【题目】设不等式组 
表示的平面区域为D，在区域D内随机取一个点，则此点到坐标原点的距离大于2的概率是 ．
【答案】
【解析】解：到坐标原点的距离大于2的点，位于以原点O为圆心、半径为2的圆外
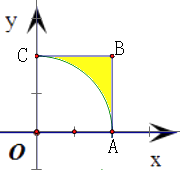
区域D： 
表示正方形OABC，（如图）
其中O为坐标原点，A（2，0），B（2，2），C（0，2）．
因此在区域D内随机取一个点P，
则P点到坐标原点的距离大于2时，点P位于图中正方形OABC内，
且在扇形OAC的外部，如图中的阴影部分
∵S正方形OABC=22=4，S阴影=S正方形OABC﹣S扇形OAC=4﹣ 
π22=4﹣π
∴所求概率为P= 
= 
所以答案是：
【考点精析】利用几何概型对题目进行判断即可得到答案，需要熟知几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
相关题目
【题目】二手车经销商小王对其所经营的某一型号二手汽车的使用年数x（0＜x≤10）与销售价格y（单位：万元/辆）进行整理，得到如表的对应数据：
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
（1）试求y关于x的回归直线方程；（参考公式： 
= 
， 
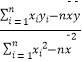=y﹣ 
）
（2）已知每辆该型号汽车的收购价格为w=0.01x3﹣0.09x2﹣1.45x+17.2万元，根据（1）中所求的回归方程，预测x为何值时，小王销售一辆该型号汽车所获得的利润L（x）最大？（利润=售价﹣收购价）
