Question

【题目】设函数f（x）=x（lnx﹣ax）（a∈R）在区间（0，2）上有两个极值点，则a的取值范围是（ ）
A.
B.
C.
D.

Answer 1

【答案】D
【解析】解：方法一：f（x）=x（lnx﹣ax），求导f′（x）=lnx﹣2ax+1，

由题意，关于x的方程a= 在区间（0，+∞）由两个不相等的实根，

令h（x）= ，h′（x）=﹣ ，

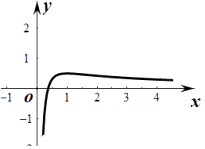
当x∈（0，1）时，h（x）单调递增，当x∈（1，+∞）单调递减，

当x→+∞时，h（x）→0，

由图象可知：函数f（x）=x（lnx﹣ax），在（0，2）上由两个极值，

只需 ＜a＜ ，

故D．

方法二：f（x）=x（lnx﹣ax），求导f′（x）=lnx﹣2ax+1，

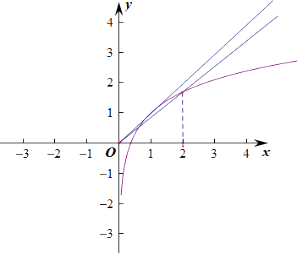
由题意，关于x的方程2ax=lnx+1在区间（0，2）由两个不相等的实根，

则y=2ax与y=lnx+1有两个交点，

由直线y=lnx+1，求导y′= ，

设切点（x0，y0）， = ，解得：x0=1，

∴切线的斜率k=1，

则2a=1，a= ，

则当x=2，则直线斜率k= ，

则a= ，

∴a的取值范围（ ， ），

故选D．

【考点精析】根据题目的已知条件，利用函数的极值与导数的相关知识可以得到问题的答案，需要掌握求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值．