题目内容
某汽车生产企业上年度生产一品牌汽车的投入成本为10万元/辆,出厂价为13万元/辆,年销售量为5000辆.本年度为适应市场需求,计划提高产品档次,适当增加投入成本,若每辆车投入成本增加的比例为 (0<
(0< <1
<1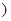 ,则出厂价相应提高的比例为0.7
,则出厂价相应提高的比例为0.7 ,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
(1)若年销售量增加的比例为0.4 ,为使本年度的年利润比上年度有所增加,则投入成本增加的比例
,为使本年度的年利润比上年度有所增加,则投入成本增加的比例 应在什么范围内?
应在什么范围内?
(2)年销售量关于 的函数为
的函数为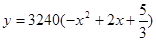 ,则当
,则当 为何值时,本年度的年利润最大?最大利润为多少?
为何值时,本年度的年利润最大?最大利润为多少?
 (0<
(0< <1
<1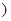 ,则出厂价相应提高的比例为0.7
,则出厂价相应提高的比例为0.7 ,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.(1)若年销售量增加的比例为0.4
 ,为使本年度的年利润比上年度有所增加,则投入成本增加的比例
,为使本年度的年利润比上年度有所增加,则投入成本增加的比例 应在什么范围内?
应在什么范围内?(2)年销售量关于
 的函数为
的函数为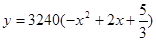 ,则当
,则当 为何值时,本年度的年利润最大?最大利润为多少?
为何值时,本年度的年利润最大?最大利润为多少?(1)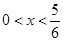 ;(2)当
;(2)当 时,本年度的年利润最大,最大利润为20000万元.
时,本年度的年利润最大,最大利润为20000万元.
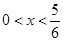 ;(2)当
;(2)当 时,本年度的年利润最大,最大利润为20000万元.
时,本年度的年利润最大,最大利润为20000万元.试题分析:(1)由题意得:本年度每辆车的投入成本为10×(1+x);
出厂价为13×(1+0.7x);年销售量为5000×(1+0.4x), 2分
因此本年度的利润为


即:
 6分
6分由
 , 得
, 得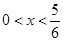 8分
8分(2)本年度的利润为

则
 10分
10分由

当
 是增函数;当
是增函数;当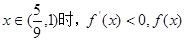 是减函数.
是减函数.∴当
 时,
时, 万元, 12分
万元, 12分因为
 在(0,1)上只有一个极大值,所以它是最大值, 14分
在(0,1)上只有一个极大值,所以它是最大值, 14分所以当
 时,本年度的年利润最大,最大利润为20000万元. 16分
时,本年度的年利润最大,最大利润为20000万元. 16分点评:研究数学模型,建立数学模型,进而借鉴数学模型,对提高解决实际问题的能力,以及提高数学素养都是十分重要的.建立模型的步骤可分为: (1) 分析问题中哪些是变量,哪些是常量,分别用字母表示; (2) 根据所给条件,运用数学知识,确定等量关系; (3) 写出
 的解析式并指明定义域。
的解析式并指明定义域。
练习册系列答案
相关题目
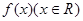 满足
满足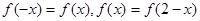 ,且当
,且当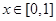 时,
时,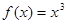 .又函数
.又函数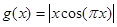 ,则函数
,则函数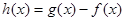 在
在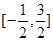 上的零点个数为 ( )
上的零点个数为 ( )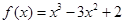 ,
,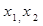 是区间
是区间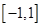 上任意两个值,
上任意两个值,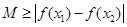 恒成立,则M的最小值是( )
恒成立,则M的最小值是( )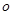 的函数关系式为:
的函数关系式为: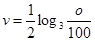 。若某条鱼想把游速提高1 m/s,它的耗氧量将增大到原来的a倍,则a=
。若某条鱼想把游速提高1 m/s,它的耗氧量将增大到原来的a倍,则a=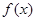 的边际函数
的边际函数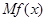 定义为
定义为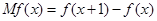 .某公司每月最多生产100台报警系统装置,生产
.某公司每月最多生产100台报警系统装置,生产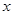 台(
台(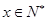 )的收入函数为
)的收入函数为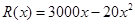 (单位:元),其成本函数为
(单位:元),其成本函数为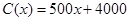 (单位:元),利润是收入与成本之差.
(单位:元),利润是收入与成本之差.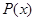 及边际利润函数
及边际利润函数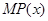 的解析式,并指出它们的定义域;
的解析式,并指出它们的定义域;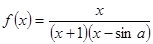 为奇函数,则
为奇函数,则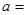 .
.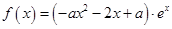 ,
,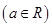
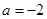 时,求函数
时,求函数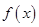 的极值;
的极值;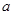 的取值范围.
的取值范围. 与每日生产产品件数
与每日生产产品件数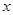 (
(
 )间的关系为
)间的关系为 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.
,每生产一件正品盈利4000元,每出现一件次品亏损2000元. (元)表示成日产量
(元)表示成日产量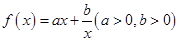 的单调性并给出证明。
的单调性并给出证明。