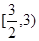题目内容
试判断函数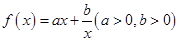 的单调性并给出证明。
的单调性并给出证明。
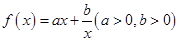 的单调性并给出证明。
的单调性并给出证明。 在
在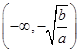 和
和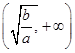 上单调递增,在
上单调递增,在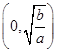 和
和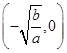 上单调递减。
上单调递减。【错解分析】在解答题中证明或判断函数的单调性必须依据函数的性质解答。特别注意定义
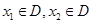
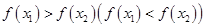 中的
中的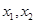 的任意性。以及函数的单调区间必是函数定义域的子集,一旦忽略定义域优先的原则,就很容易出错。
的任意性。以及函数的单调区间必是函数定义域的子集,一旦忽略定义域优先的原则,就很容易出错。【正解】因为
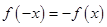 即函数
即函数 为奇函数,
为奇函数,所以只需判断函数
 在
在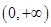 上的单调性即可。
上的单调性即可。设
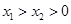 ,
,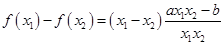
由于
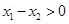
故当
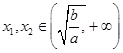 时
时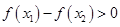 ,此时函数
,此时函数 在
在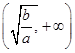 上增函数,
上增函数,同理可证函数
 在
在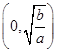 上为减函数。
上为减函数。又由于函数为奇函数,故函数在
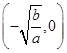 为减函数,在
为减函数,在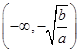 为增函数。
为增函数。综上所述:函数
 在
在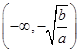 和
和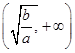 上分别为增函数,在
上分别为增函数,在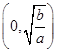 和
和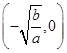 上分别为减函数.
上分别为减函数.【点评】证明或判断函数的单调性要从定义出发,应注意步骤的规范性及树立定义域优先的原则。
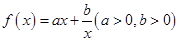 是一种重要的函数模型,要引起重视并注意应用。但注意本题中不能说
是一种重要的函数模型,要引起重视并注意应用。但注意本题中不能说 在
在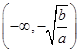
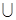
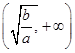 上为增函数,在
上为增函数,在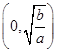
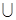
 上为减函数,在叙述函数的单调区间时不能在多个单调区间之间添加符号“∪”和“或”,
上为减函数,在叙述函数的单调区间时不能在多个单调区间之间添加符号“∪”和“或”,
练习册系列答案
相关题目
 (0<
(0< ,则出厂价相应提高的比例为0.7
,则出厂价相应提高的比例为0.7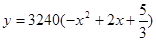 ,则当
,则当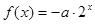 与
与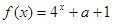 的图象有交点,则
的图象有交点,则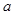 的取值范围是( )
的取值范围是( )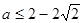 或
或 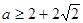
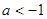
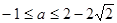
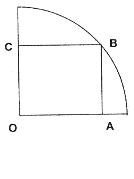
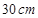 的
的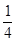 圆形(
圆形( 为圆心)铝皮上截取一块矩形材料
为圆心)铝皮上截取一块矩形材料 ,其中点
,其中点 在圆上,点
在圆上,点 、
、 在两半径上,现将此矩形铝皮
在两半径上,现将此矩形铝皮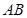 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长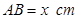 ,圆柱的体积为
,圆柱的体积为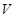
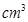 .
.
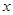 的函数关系式,并指出定义域;
的函数关系式,并指出定义域;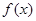 是定义在
是定义在 上的单调增函数,满足
上的单调增函数,满足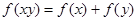 ,
,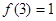 ,
,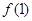 ;
;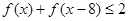 ,求
,求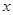 的取值范围。
的取值范围。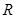 上的函数
上的函数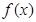 满足
满足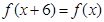 ,当
,当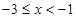 时,
时,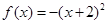 ,当
,当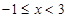 时,
时,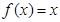 ,则
,则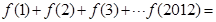
 上是增函数,那么实数a的取值范围是( )
上是增函数,那么实数a的取值范围是( )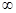 )
)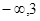 )
)