题目内容
【题目】一批材料可以建成100m长的围墙,现用这些材料在一边靠墙的地方围成一块封闭的矩形场地,中间隔成3个面积相等的小矩形(如图),则围成的矩形场地的最大总面积为(围墙厚度忽略不计)m2 . 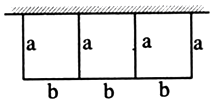
【答案】625
【解析】解:设每个小矩形的高为am,则长为b= ![]() (100﹣4a)m,记面积为Sm2
(100﹣4a)m,记面积为Sm2
则S=3ab=a(100﹣4a)=﹣4a2+100a=﹣4(a﹣ ![]() )2+625(0<a<25)
)2+625(0<a<25)
∴当a=12.5时,Smax=625(m2)
∴所围矩形面积的最大值为625m2
所以答案是625.
【考点精析】解答此题的关键在于理解基本不等式在最值问题中的应用的相关知识,掌握用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、三相等”.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目