题目内容
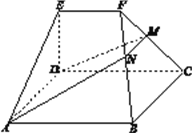
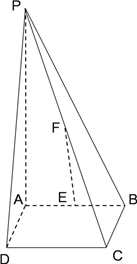
【题目】如图,三棱锥![]() ,侧棱
,侧棱![]() ,底面三角形
,底面三角形![]() 为正三角形,边长为
为正三角形,边长为![]() ,顶点
,顶点![]() 在平面
在平面![]() 上的射影为
上的射影为![]() ,有
,有![]() ,且
,且![]() .
.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)线段![]() 上是否存在点
上是否存在点![]() 使得
使得![]() ⊥平面
⊥平面![]() ,如果存在,求
,如果存在,求![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.

【答案】(Ⅰ)见解析;(Ⅱ)![]() ;(Ⅲ)见解析.
;(Ⅲ)见解析.
【解析】试题分析:(1)证线面平行,则要在平面![]() 找一线与之平行即可,显然分析
找一线与之平行即可,显然分析![]() 即得证,(2)求二面角可借助空间直角坐标系将两个平面的法向量一一求出,再根据向量的数量积公式便可求解(3)存在问题可以根据结论反推即可,容易得因为
即得证,(2)求二面角可借助空间直角坐标系将两个平面的法向量一一求出,再根据向量的数量积公式便可求解(3)存在问题可以根据结论反推即可,容易得因为![]() ,所以
,所以![]() 与
与![]() 不垂直,故不存在
不垂直,故不存在
试题解析:
(Ⅰ)因为![]() ,且
,且![]() ,
, ![]() ,所以
,所以![]() ,
,
所以![]() .
.
因为![]() 为正三角形,所以
为正三角形,所以![]() ,
,
又由已知可知![]() 为平面四边形,所以
为平面四边形,所以![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)由点![]() 在平面
在平面![]() 上的射影为
上的射影为![]() 可得
可得![]() 平面
平面![]() ,
,
所以![]() ,
, ![]() .
.
以![]() 分别为
分别为![]() 建立空间直角坐标系,则由已知可知
建立空间直角坐标系,则由已知可知![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
平面![]() 的法向量
的法向量![]() ,
,
设![]() 为平面
为平面![]() 的一个法向量,则
的一个法向量,则
由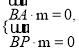 可得
可得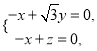
令![]() ,则
,则![]() ,所以平面
,所以平面![]() 的一个法向量
的一个法向量![]() ,
,
所以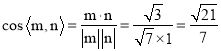 ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
(Ⅲ)由(Ⅱ)可得![]() ,
, ![]() ,
,
因为![]() ,
,
所以![]() 与
与![]() 不垂直,
不垂直,
所以在线段![]() 上不存在点
上不存在点![]() 使得
使得![]() ⊥平面
⊥平面![]() .
.

练习册系列答案
相关题目
【题目】某单位附近只有甲、乙两个临时停车场,它们各有![]() 个车位,为了方便市民停车,某互联网停车公司对这两个停车场,在某些固定时刻的剩余停车位进行记录,如下表:
个车位,为了方便市民停车,某互联网停车公司对这两个停车场,在某些固定时刻的剩余停车位进行记录,如下表:
时间 停车场 |
|
|
|
|
|
|
甲停车场 |
|
|
|
|
|
|
乙停车场 |
|
|
|
|
|
|
如果表中某一时刻剩余停车位数低于该停车场总车位数的![]() ,那么当车主驱车抵达单位附近时,该公司将会向车主发出停车场饱和警报.
,那么当车主驱车抵达单位附近时,该公司将会向车主发出停车场饱和警报.
(1)假设某车主在以上六个时刻抵达单位附近的可能性相同,求他收到甲停车场饱和警报的概率;
(2)从这六个时刻中任选一个时刻,求甲停车场比乙停车场剩余车位数少的概率;
(3)当乙停车场发出饱和警报时,求甲停车场也发出饱和警报的概率.