题目内容
【题目】以下四个命题中是假命题的是
A. “昆虫都是6条腿，竹节虫是昆虫，所以竹节虫有6条腿”此推理属于演绎推理.
B. “在平面中，对于三条不同的直线
， 
， 
，若
， 
则
，将此结论放到空间中也成立” 此推理属于合情推理.
C. “
”是“函数
存在极值”的必要不充分条件.
D. 若
，则
的最小值为
.
【答案】D
【解析】易知“昆虫都是6条腿，竹节虫是昆虫，所以竹节虫有6条腿”此推理属于演绎推理，“在平面中，对于三条不同的直线
， 
， 
，若
， 
则
，将此结论放到空间中也成立” 此推理属于合情推理中的类比推理，故选项A、B为真命题；因为
存在极值
有零点，则
，所以“
”是“函数
存在极值”的必要不充分条件，即选项C正确；若
，则
， 
，但
，故选项D错误；故选D.
【题目】某地最近十年粮食需求量逐年上升，下表是部分统计数据：
年份 | 2006 | 2008 | 2010 | 2012 | 2014 |
需求量(万吨) | 236 | 246 | 257 | 276 | 286 |
(1)利用所给数据求年需求量与年份之间的回归方程
＝
x＋
；
(2)利用(1)中所求出的直线方程预测该地2018年的粮食需求量．
【题目】为了监控某种零件的一条生产线的生产过程，检验员每天从该生产线上随机抽取16个零件，并测量其尺寸（单位：cm）．根据长期生产经验，可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布
．
（1）假设生产状态正常，记X表示一天内抽取的16个零件中其尺寸在
之外的零件数，求
；
（2）一天内抽检零件中，如果出现了尺寸在
之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查．
下面是检验员在一天内抽取的16个零件的尺寸：
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得
， 
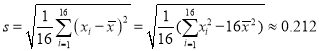，其中
为抽取的第
个零件的尺寸， 
．
用样本平均数
作为
的估计值
，用样本标准差
作为
的估计值
，利用估计值判断是否需对当天的生产过程进行检查？剔除
之外的数据，用剩下的数据估计
和
（精确到0.01）．
附：若随机变量
服从正态分布
，则
，
， 
．
【题目】“共享单车”的出现，为我们提供了一种新型的交通方式．某机构为了调查人们对此种交通方式的满意度，从交通拥堵不严重的
城市和交通拥堵严重的
城市分别随机调查了20个用户，得到了一个用户满意度评分的样本，并绘制出茎叶图（如图所示）：
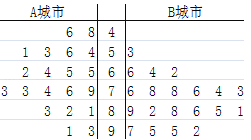
若得分不低于80分，则认为该用户对此种交通方式“认可”，否则认为该用户对此种交通方式“不认可”，请根据此样本完成此
列联表，并据此样本分析是否有
的把握认为城市拥堵与认可共享单车有关：
|
| 合计 | |
认可 | |||
不认可 | |||
合计 |
附：参考数据：（参考公式：
）
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
