题目内容
【题目】设命题![]() 是
是![]() 的必要而不充分条件;
的必要而不充分条件;
设命题![]() 实数
实数![]() 满足方程
满足方程![]() 表示双曲线.
表示双曲线.
(1)若“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:
首先求得命题p,q为真是参数m的取值范围,然后结合题意得到关于实数m的不等式,求解不等式可得:
若“![]() ”为真命题,实数
”为真命题,实数![]() 的取值范围是
的取值范围是![]() ;
;
若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
由![]() ,得
,得![]()
命题![]() 真时,则
真时,则![]() ,得
,得![]()
∴命题![]() 假时,
假时, ![]() ,
,
命题![]() 真时,得
真时,得![]() ,解得
,解得![]() 或
或![]() ,
,
命题![]() 假时,
假时, ![]()
(1)若“![]() ”为真命题,则
”为真命题,则![]() 真
真![]() 真,所以
真,所以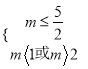 ,
,
所以![]() 或
或![]()
即实数![]() 的取值范围为:
的取值范围为: ![]()
(2)∵![]() 为假,
为假, ![]() 为真,∴
为真,∴![]() 一真一假.
一真一假.
当![]() 真
真![]() 假时,则
假时,则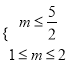 ,所以
,所以![]() ;
;
当![]() 假
假![]() 真时,则
真时,则 ,所以
,所以![]() .
.
综上可知,实数![]() 的取值范围为:
的取值范围为: ![]() .
.

练习册系列答案
相关题目
【题目】某高中在校学生2 000人,高一年级与高二年级人数相同并且都比高三年级多1人.为了响应市教育局“阳光体育”号召,该校开展了跑步和跳绳两项比赛,要求每人都参加而且只参加其中一项,各年级参与项目人数情况如下表:
年级 项目 | 高一年级 | 高二年级 | 高三年级 |
跑步 | a | b | c |
跳绳 | x | y | z |
其中a∶b∶c=2∶3∶5,全校参与跳绳的人数占总人数的![]() . 为了了解学生对本次活动的满意度,采用分层抽样从中抽取一个200人的样本进行调查,则高二年级中参与跑步的同学应抽取多少人?
. 为了了解学生对本次活动的满意度,采用分层抽样从中抽取一个200人的样本进行调查,则高二年级中参与跑步的同学应抽取多少人?