Question

【题目】对于函数，若函数是增函数，则称函数具有性质A．

若，求的解析式，并判断是否具有性质A；

判断命题“减函数不具有性质A”是否真命题，并说明理由；

若函数具有性质A，求实数k的取值范围，并讨论此时函数在区间上零点的个数．

Answer 1

【答案】（1），具有性质A；（2）假命题；（3）详见解析.

【解析】

由，结合即可得出解析式，和单调性，进而可得出结果；

判断命题“减函数不具有性质A”，为假命题，举出反例即可，如；

若函数具有性质A，可知 在为增函数，进而可求出实数k的取值范围；再令，则在区间上零点的个数，即是的根的个数，结合k的取值范围，即可求出结果.

解：，，

在R上递增，可知具有性质A；

命题“减函数不具有性质A”，为假命题，比如：，

在R上递增，具有性质A；

若函数具有性质A，

可得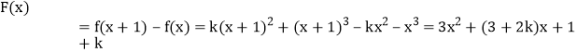

在递增，可得，解得；

由，可得，即，

可得，时显然成立；

时，，

由在递减，且值域为，

时，或1，有三解，3个零点；

当时，，即，可得，1个零点；

当时，，t有一解，x两解，即两个零点；

当，且时，无解，即x无解，无零点．