题目内容
【题目】设函数
.
（1）讨论函数
的单调性；
（2）若
，不等式
恒成立，求实数
的取值范围.
【答案】（1）在区间
上是减函数，在区间
上是增函数；（2）
【解析】
（1）利用导函数的正负讨论函数的单调性；
（2）不等式
化为
，结合（1）的结论，分析函数单调性，讨论函数最值，根据不等式恒成立求参数的取值范围.
解：（1）
所以
为增函数，又因为
所以，当
时，
；当
时，
所以，函数
在区间
上是减函数，在区间
上是增函数
（2）不等式化为
设
，
由（1）可知
是
上的增函数，
因为
，所以，当
，函数g(x)在区间上的增函数
所以
，所以当
时符合题意.
当
，
，所以存在
，使得
；
并且当
；
当
；
所以函数
在区间
上是减函数，在区间
上是增函数
最小值为
，不等式不恒成立
综上，使得命题成立的实数
的取值范围是
练习册系列答案
相关题目
【题目】已知函数
的定义域为[－1，5]，部分对应值如下表，的导函数
的图象如图所示，下列关于的命题正确的是（ ）
|
| 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
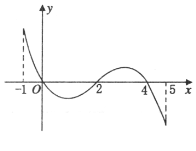
A.函数的极大值点为0，4；
B.函数在[0，2]上是减函数；
C.如果当
时，的最大值是2，那么
的最大值为4；
D.函数
的零点个数可能为0、1、2、3、4个．
